If it is assumed that every consumer within a particular region has the same 'valuation' for a certain product, and consumers will purchase no more than one unit of the product, is the market demand curve perfectly elastic (horizontal)?
Any insight would be appreciated.
Let $v_i$ be the valuation that the $i$-th consumer has for the product, and $v^*$ the common valuation of the product, where the $v$'s are measured in monetary units, and are assumed continuous. Consumers are here assumed binary -they either purchase $0$ or $1$ (i.e. the product is indivisible). We assume that if the valuation is equal to the price, they do want to purchase the product.
Write the indicator function $I\{v_i\geq p\}$, that takes the value $1$ if the valuation is greater or equal than the price (and so the consumer will want to buy the one unit of product. Let there be $N$ consumers. Then, demand can be expressed as
$$Q^{d} = \sum_{i=1}^NI\{v_i\geq p\}$$
and since the valuation is assumed common to all,
$$Q^{d} = N\cdot I\{v^*\geq p\}$$
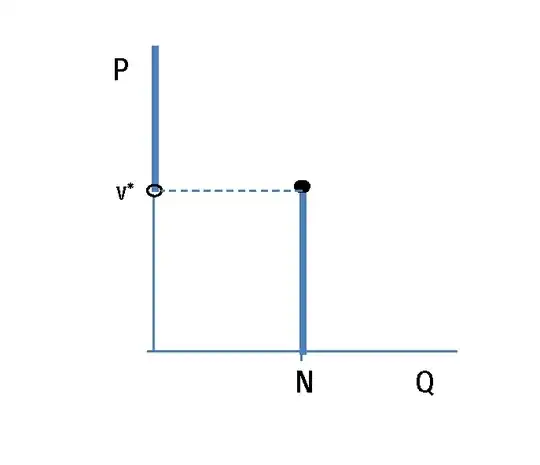
We see that if $p\leq v^*$, quantity demanded will be equal to $N$, while if $p> v^*$ quantity demanded will be equal to $0$.
Diagrammatically, this gives
A horizontal demand curve could be assembled if you had an sufficiently large number of customers who will buy of the price is $p*$ or less. When $p \leq p*$ then they purchase all units available until they reach the limiting factor of the quantity supplied. At any point, they purchase $Q_s$ units at a price of $p*$. The good would then be perfectly inelastic, a flat demand curve.
As for why this behavior would exist, I imagine perhaps the good is a necessary input into a widely available machine. This machine produces another good worth only $p*$ plus the cost of other inputs. There are probably better examples for perfectly inelastic goods, but at the moment I'm drawing a relative blank.
