0

Consider a very simple economy with two agents (A, B) and two goods ($x$, $y$). Agent A has utility $u_a = \min \{x_a, 2y_a\}$; agent B symmetrically has utility $u_b = \min \{2x_b, y_b\}$. Suppose that there are 3 units of $x$ and 3 units of $y$ in total.

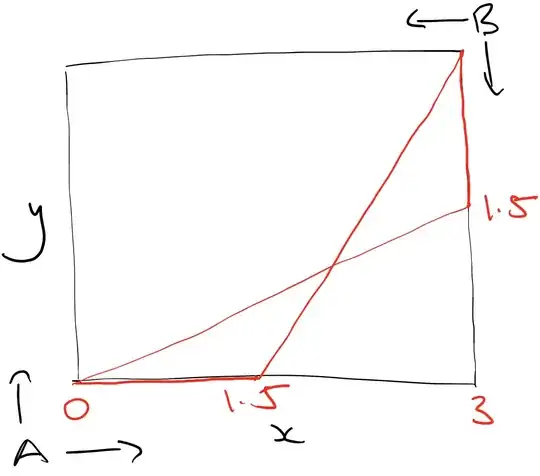
It seems that, if $x_a = 2y_a$ and endowments are exhausted, then the allocation is efficient. In addition, if $2x_b = y_b$ and endowments are exhausted, i.e. $2(3 - x_a) = 3 - y_a$, then the allocation is also efficient. Finally, there seem to be some efficient allocations on the boundary of the feasible set. Plotting these yields

enter image description here

Can I confirm that the red lines do indeed depict the set of efficient allocations? I'm not looking for a formal proof, but just a confirmation that I haven't overlooked anything in this problem.

afreelunch
  • 856
  • 3
  • 9
  • You can follow the approach posted here. I think it'll help: https://youtu.be/HzJyV5zBaPg – Amit Jan 07 '23 at 16:07

1 Answers1

2

The diagram of the edge worth box is correct and yes indeed the points on two red lines are Pareto efficient but in addition to that the points contained in the area between these two red lines (two triangles formed only by the red lines) are also Pareto efficient allocations.

Amit Ranjan
  • 36
  • 2