6

UPDATE
I was not thinking straight anymore and got totally confused after working hours on my equations. The point is, I have an unstable system, but I force it on the stable path. After realizing that crucial point everything made perfect sense.

Problem

(I fixed some major errors)

I'm having a two dimensional system with dynamics \begin{align} \dot{k} &= \frac{1}{1+\frac{1}{\rho}} - \frac{1}{1+\lambda}\\ \dot{\lambda} &= \rho\lambda - \frac{1}{k}. \end{align} Where $k\in[0,2]$ is the state, and $\lambda$ the costate. There is a (symmetric) fixed point $E(\tilde{k},\tilde{\lambda})$ at $\tilde{\lambda} = \frac{1}{k\rho}$ which yields $\tilde{k}=1$. 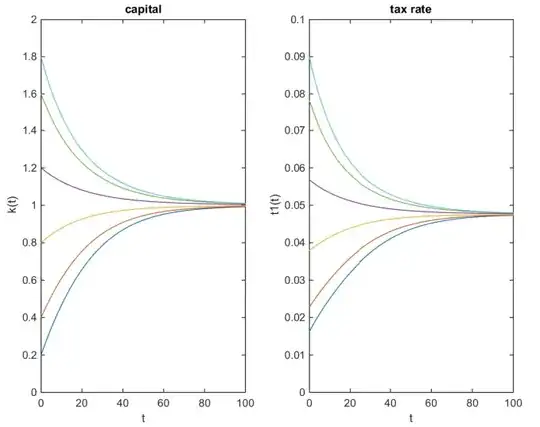The Jacobian at the fixed point is given by \begin{align} J_E = \begin{bmatrix}0,& \frac{1}{\left(\frac{1}{\rho}+1\right)^2}\\ 1,& \rho\end{bmatrix}_E \end{align} I get two eigenvalues which are opposite in sign \begin{align} (\mu_1,\mu_2)=\left(\frac{p(p + \sqrt{p^2 + 2p + 5}+ 1}{2(p + 1)},\frac{p(p - \sqrt{p^2 + 2p + 5}+ 1}{2(p + 1)}\right) \end{align} where $\rho\in\mathbb{R}_{++}$ (time preference rate). The first eigenvalue is always positive ($\mu_1>0$) and the second one is always negative ($\mu_2<0$). So it is an unstable saddle,right? Nonetheless the system is stable. How is that possible, cause I used to think that it must be unstable? The image shows the evolution of the state and the control which is a function of the costate. 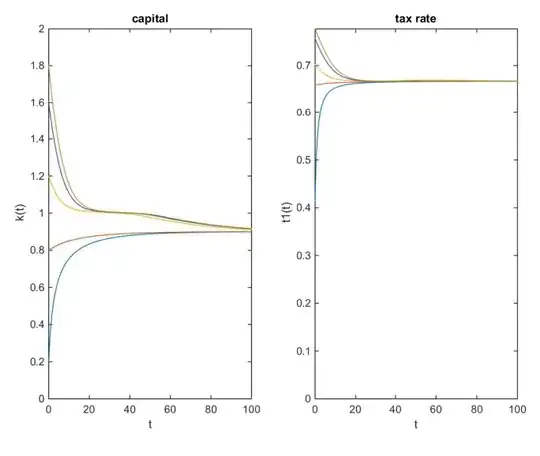($\rho = 0.05$) enter image description here

For reference I add figures with $\rho=2,5$. The first one seems to converge to a different fixed point $k<1$ (I didn't solve for that one, cause I deal with a symmetric situation; I think there are three in total).

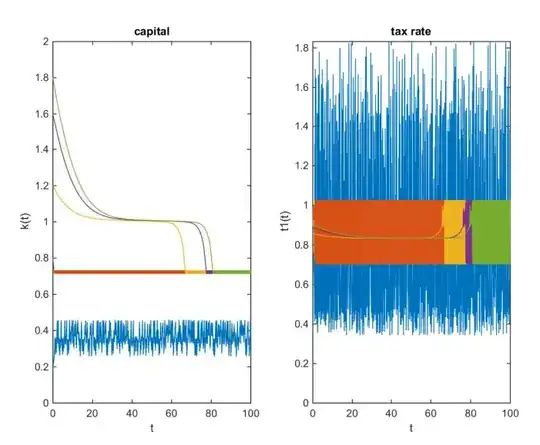
enter image description here

And the second picture shows a strange attractor? Which I actually quite like cause of its chaotic stability. For $k\in[0,3]$ the policy function $\tau_1(k)$ is quite weird.

enter image description here

Alecos Papadopoulos
  • 33,814
  • 1
  • 48
  • 116
clueless
  • 1,579
  • 10
  • 21
  • 2
    Perhaps you could include the equations describing the dynamics?

    A guess: You are in a discrete time model, not a continuous one. The stability criterion for discrete time is that the absolute value of the eigenvalues are smaller than one. See http://en.wikipedia.org/wiki/Lyapunov_stability#Stability_for_linear_state_space_models

     – Giskard Apr 19 '15 at 09:58
  • You've nailed it. – clueless Apr 19 '15 at 10:30
  • Dont delete the question, there's valuable information here that might be useful for future visitors - and that's all StackExchange is about, generating a stock of information. Perhaps instead just accept the answer and move on :) – FooBar Apr 21 '15 at 15:22

2 Answers2

2

If you have are trying to discretize the continuous time model $$ \dot{\textbf{x}} = A\textbf{x}, $$ then in discrete time you will have $$ \textbf{x}_{t+1} = B \textbf{x}_t $$ but $A\neq B$, since $A$ describes the change in $\textbf{x}$ while $B$ describes the next value of $\textbf{x}$, not just the change. However $$ \Delta\textbf{x}_t = \textbf{x}_{t+1} - \textbf{x}_t = B \textbf{x}_t - \textbf{x}_t = (B-I) \textbf{x}_t $$ This new matrix $B-I$ would correspond to $A$.

(From this you can also see why the stability criterion is different.)

Given your equations \begin{eqnarray*} \dot{k} & = & \frac{1}{1+\frac{1}{\rho}} - \frac{1}{1+\lambda} \\ \\ \dot{\lambda} & = & \rho \lambda - \frac{1}{k} \end{eqnarray*} the equations for the discrete modell would be \begin{eqnarray*} k_{t+1} & = & k_t + \frac{1}{1+\frac{1}{\rho}} - \frac{1}{1+\lambda_t} \\ \\ \lambda_{t+1} & = & \lambda_t + \rho \lambda_t - \frac{1}{k_t}. \end{eqnarray*} You will have to calculate the Jacobian of this system to determine stability.

Giskard
  • 29,387
  • 11
  • 45
  • 76
1

I find that the system is saddle-path stable.

Setting $z\equiv 1/k$ we get

\begin{eqnarray*} \dot{z} & = & -z^2\left(\frac{\rho}{1+\rho} - \frac{1}{1+\lambda}\right) \\ \\ \dot{\lambda} & = & \rho \lambda - z \end{eqnarray*}

The fixed point is $E=\{z^*, \lambda^*\} = \{1, 1/\rho\}$

The Jacobian of this system evaluated at the steady state is

\begin{align} J_E = \begin{bmatrix}0& -\frac{\rho^2}{(1+\rho)^2}\\ -1& \rho\end{bmatrix} \end{align}

The determinant is

$${\rm det}(J_E) = 0-\frac{\rho^2}{(1+\rho)^2} < 0$$

and when the determinant of the Jaconbian in a two-by-two system is negative, the system is saddle-path stable (and so mathematically speaking, unstable), irrespective of whether the trace of the Jacobian (here equal to $\rho>0$) is positive, negative, or zero.

Perhaps this could be helpful.

Alecos Papadopoulos
  • 33,814
  • 1
  • 48
  • 116
  • Thanks. Say, I don't know whether I have a real or complex eigenvalue. But I know $\det(J_E)<0$ and is real. Is that sufficient to inference on a saddle and/or real eigenvalues? From the link you posted I'd guess so, since $\det(J_E)<0$ cannot hold for complex eigenvalues?! – clueless Apr 21 '15 at 16:14
  • The point is, that I want to save space and do not want to write down those long eigenvalues and show that they are real and opposite in sign for all $\rho$. And the $\det(J_E)<0$ is way shorter and smoother. I actually do have an additional parameter which is implicity set to unity here, but would occur as well. – clueless Apr 21 '15 at 16:23
  • @clueless That's right, if the determinant of the Jacobian is negative, then you don't get complex roots, that's very easy to show, if you look at how the discriminant of the characteristic equation is calculated. Having a positive determinant is necessary although not sufficient, for complex roots. – Alecos Papadopoulos Apr 21 '15 at 16:31