-1

enter image description here

my current thinking is i have to dis/prove two things

  1. cardinality
  2. continuity but im not sure about how it would apply since the above is a natural X natural choice space

I know cardinality of natural choice space = cardinality of rational numbers, but im not sure how I can relate that to representation in a utility function

Im not sure about continuity because epsilon balls around numbers in a natural space doesnt include anything else

Michael Greinecker
  • 12,207
  • 1
  • 24
  • 36
theshadowers
  • 21
  • 2
  • 1
    Have you tried writing down a few bundles and seeing if there is a way to compare them? Try out out some examples and it should be clear if such a representation is possible. – Walrasian Auctioneer Jan 25 '22 at 18:58
  • 1
    No it doesn't. The link you provide shows an example where they are comparing real to rational as a proof, whereas my question is set in the natural choice space @Giskard – theshadowers Jan 25 '22 at 19:03
  • @WalrasianAuctioneer yeah, the lexicographic preference can be compared by drawing but im not sure how i can prove that – theshadowers Jan 25 '22 at 19:05
  • Sorry, mistake! But why are you bringing continuity into this? It is not required that $U$ is continuous, is it? – Giskard Jan 25 '22 at 19:06
  • @Giskard my lecture notes state that discontinuous preferences cannot be represented by a utility function, hence the continuity argument – theshadowers Jan 25 '22 at 19:10
  • I am afraid your lecture notes are mistaken in this instance. – Giskard Jan 25 '22 at 19:11
  • E.g., the sign function defines discontinuous preferences over $\mathbb{R}$. – Giskard Jan 25 '22 at 19:16
  • @Giskard okay, if we assume to ignore the continuity statement, do you have any suggestions as to how I would proceed with the first point? – theshadowers Jan 25 '22 at 19:20
  • I posted an answer 10 minutes ago (: – Giskard Jan 25 '22 at 19:20
  • At first I linked the wrong question, but here is a true duplicate: Lexicographic Preference Relation on the QxR – Giskard Jan 25 '22 at 19:21
  • @Giskard Can I ask about the significance of the first line in your answer below? I don't really understand how we can map the entire natural plane in [0,1) – theshadowers Jan 25 '22 at 19:21
  • You don't understand the function that assigns $1 - 1/(y+1)$ to $y$? What do you not understand about it? Do you think this can go under 0 or above 1? Note that it is not about the natural plane, just natural numbers. – Giskard Jan 25 '22 at 19:21
  • @Giskard Sorry, not the function, but I dont think I understand the significance or implications of Take a strictly increasing mapping f:N→[0,1) What are we doing here and why can we map the natural plane as [0,1)? – theshadowers Jan 25 '22 at 19:24
  • It does not map the natural plane, just natural numbers. I suggest you take
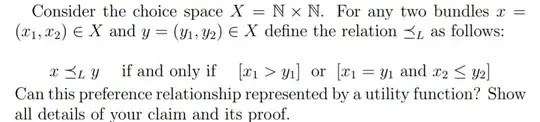
    WalrasianAuctioneer's advice and experiment by plugging in some numbers, e.g., is (2,0) preferred to (1,99) according to this function?     – Giskard Jan 25 '22 at 19:25
  • @Giskard okay after prolonged thinking I believe I understand most of it. do you think it is necessary for me to state the cardinality stuff? as the question asks to show all details of your claim and proof – theshadowers Jan 25 '22 at 20:11
  • I cannot speak for your university program, but I am sure you can talk about the exact requirements with your professor. – Giskard Jan 25 '22 at 20:28
  • @Giskard thank you so much for your help! I understand it now – theshadowers Jan 25 '22 at 21:47

1 Answers1

4

Take a strictly increasing mapping $f:\mathbb{N} \to [0,1)$, such as $$ f(y) = 1 - \frac{1}{y+1}. $$ Then $$ U(x,y) = x + f(y) $$ represents the Lexicographic preference in the $\mathbb{N}^2$ choice space.

Giskard
  • 29,387
  • 11
  • 45
  • 76