1

I note that someone did ask a similar question here (Thin indifference curves), but I didn't fully understand the answer, and my question refers specifically to my textbook.

In my textbook, Jehle & Reny, the axiom of continuity is defined as follows:

Excerpt from Jehle & Reny, page 8

Figure 1.1

Why does continuity alone preclude an indifference region with "thickness"? I would've thought the preference relation for a consumer who is indifferent between all combinations of x1 and x2 still satisfies continuity, and that non-satiation is required to rule out "thick" indifference curves.

Am I misunderstanding something (highly likely)?

cashman
  • 39
  • 3
  • 4
    It does not. It just implies that indifference curves are closed sets. – Michael Greinecker Jan 05 '22 at 11:41
  • Ahh..... hence the dashed lines in the diagram. That makes sense. Thank you. – cashman Jan 05 '22 at 11:53
  • 3
    Yes, compare the figure with Fig. 1.2., where the boundary lines are no longer dashed, but the curve is still "thick". – VARulle Jan 05 '22 at 12:03
  • Thank you!

    So does this mean that the axiom of continuity guarantees the existence of a (closed) indifference set?

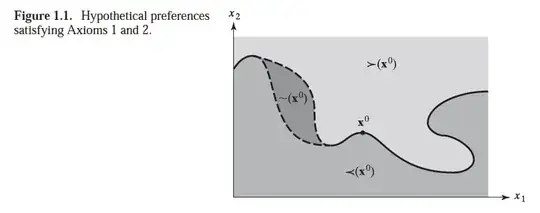
     – cashman Jan 05 '22 at 12:05
  • 3
    Yes, exactly. Because an indifference curve through a point is the intersection of the corresponding weakly-better-set and weakly-worse-set, and these are closed by the continuity assumption. – Michael Greinecker Jan 05 '22 at 13:52
  • 1
    @MichaelGreinecker Please post answers as answers. – Giskard Jan 05 '22 at 15:22
  • Thank you very much @MichaelGreinecker.

    I need to spend some time getting my head around why this image (figure 1.1) doesn't violate the axiom of completeness. Ie, won't a point on the dashed line fail to satisfy the axiom of completeness?

    I begin my graduate level micro class in two months so I'm digging deep into these concepts in preparation.

     – cashman Jan 05 '22 at 22:06
  • @cashman Have you studied the math appendix of Jehle & Reny? I think it is pretty good, this specific problem is more a math than an econ problem. And best of luck with graduate micro! – Michael Greinecker Jan 05 '22 at 22:54
  • Thank you! I just read that relevant sections of the appendix.

    So if there is a consumption bundle that lies exactly on the upper dashed portion of the indifference curve depicted in figure 1.1, obviously this bundle is necessarily weakly preferred to x0, thus satisfying the axiom of completeness. But how do we know if it is ~0 or strictly preferred to x0? We know there is a gap in continuity (previous discussion). I suppose this is the subtle distinction between the concepts of continuity and completeness. Completeness doesn't care if it is > or ~, only that it is >~. Is that correct?

     – cashman Jan 06 '22 at 00:02
  • 2
    @Giskard, I will write a polished answer to my own question once I've ironed out my understanding. Good practice for me! – cashman Jan 06 '22 at 00:26

1 Answers1

1

To answer my own question, continuity can allow for thick indifference curves, but it precludes open areas, such as the dotted line shown in the picture.

Continuity guarantees the existence of a closed indifference set, that being the intersection of the weakly-better-than-set and weakly-worse-than-set.

cashman
  • 39
  • 3