It's frequently useful in physics and engineering applications; are there any applications in theoretical economics? (If not, were there any attempts at incorporating CA that just never caught on?)
-
1Maybe in econometric theory? I've only seen complex numbers when using things like characteristic functions, which can be useful in probability theory. – Pburg Nov 19 '14 at 04:55
-
1Following @Pburg, complex numbers definitely "show up" in economics in as much as it uses mathematical tools which naturally generate complex number (such as when we linearize macroeconomic models around an equilibrium and obtain complex eigenvalues). However, I am unaware of any model or theory which "directly" rely on the properties of complex numbers as modelling tools. Maybe you could clarify your question : are you looking for the second or the first instance of use of complex analysis in economics? – Martin Van der Linden Nov 19 '14 at 05:46
-
Maybe in models which use differential equation. Once the eigenvalues are found, they determine dynamics like spirals. – Lex Nov 19 '14 at 10:30
-
1Using trivial properties of complex numbers is not complex analysis by any stretch. Otherwise pretty much all of real analysis is complex analysis---complex measures, Fourier transforms, etc. At the bare minimum, one needs to step into the world of holomorphic functions to be using complex analysis. Yes, there are some macro models where complex analysis is relevant. – Michael Nov 19 '14 at 14:04
-
This question needs some clarification. Does the OP have specific examples of complexity used in physics and engineering applications? Just to get an idea of what is being asked. OP isn't asking about complexity analysis from computer science, right? (As in, complexity of algorithms?) – CompEcon Nov 20 '14 at 16:20
-
I think the OP was pretty clear in what he/she was asking; this just happens to be a somewhat "weak" question that could be answered with a simple Google search. One vote from me to repoen. – daOnlyBG Nov 21 '14 at 02:30
-
1Pretty clear what the OP is asking. I can provide a specific answer if on-hold is removed. – Michael Nov 22 '14 at 23:59
-
Why is the question on hold? It's a clear question. – Nov 23 '14 at 13:03
-
1http://books.google.com/books?id=hg7EQdzI_TQC&pg=PA1136&lpg=PA1136#v=onepage&q&f=false An example of using complex numbers (though it's Sargent and Hansen who use mathematical tools very frequently!) So things like analyzing impulse response in frequency domain, which is used in electrical engineering but definitely also relevant in economics. – John Luke Nov 26 '14 at 21:38
-
I think the main use of complex analysis in economics is by grad school applicants, who use good good grades in analysis courses to signal their mathematical aptitude to admissions committees. – Ubiquitous Nov 28 '14 at 19:49
-
This comes probably closest to being a genuine example: http://www.nbs.rs/export/sites/default/internet/latinica/90/90_9/AlexeiBulatov_wp.pdf – Michael Greinecker Jul 04 '15 at 00:34
4 Answers
It should be pointed out that just because one encounters complex numbers does not mean one is doing "complex analysis", e.g. complex eigenvalues, complex Borel measures, Fourier transforms, etc. where trivial properties of complex numbers come up.
Complex analysis is a very focused subject unlike, say, real analysis, which is eclectic by comparison. At its core are holomorphic functions of one or more complex variables.
This paper
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=932693
is a specific instance of an economic model where complex analysis is used. The model solution technique used there is the identification between holomorphic functions on the unit disk and their continuation on the boundary. (The resulting function space is called the Hardy space, which contains the players' strategy spaces in the game being played in the paper.)
- 2,619
- 13
- 22
Complex numbers and complex analysis do show up in Economic research. For example, many models imply some difference-equation in state variables such as capital, and solving these for stationary states can require complex analysis.
However, as others already emphasized, complex analysis is mostly a byproduct of solving equations. I'm not familiar with any paper where complex analysis is at the heart of the model.
- 10,712
- 1
- 29
- 60
-
To add to the answer, one way to study difference equations is to use generating functions, which is where complex analysis comes in. – Jyotirmoy Bhattacharya Nov 21 '14 at 14:27
-
For example, what equations in economics (outside of finance) have been solved by complex analysis. That would improve your answer, if you could list the examples you are aware of, at least in this limited sense. – Nov 23 '14 at 13:37
As described in the comments, you could maybe count instances in probability theory, econometrics, PDEs, or numerical analysis. But in general, besides using trivial properties of complex numbers (as @Micheal stated), the answer is no.
- 9,345
- 5
- 30
- 80
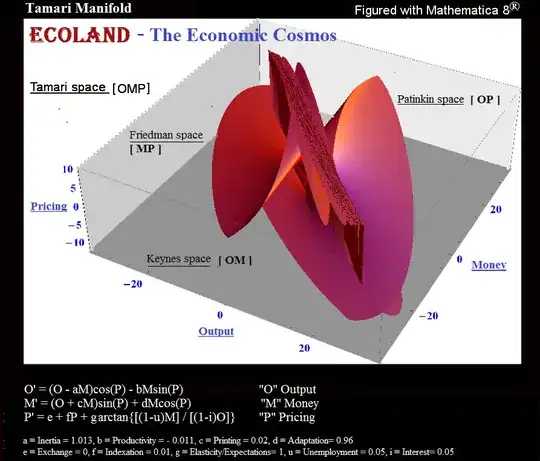 Ben Tamari (1997). "Conservation and Symmetry Laws and Stabilization Programs in Economics." English.
Ben Tamari (1997). "Conservation and Symmetry Laws and Stabilization Programs in Economics." English.
Conservation and Symmetry Laws and Stabilization Programs in Economics Abstract: An autonomous economic system, i.e., a country, tends to be a conservative and a symmetrical system in Keynes space (Output, Money and Time [Ot, Mt ; t]), and can therefore be represented as a complex numbers system. This presentation makes it possible to aggregate (or disaggregate) the system at all levels, from the individual to the most general aggregate (and vice versa). It also offers a simultaneous solution to the problem of allocating and distributing useful resources in the market.
- 19
- 1