10

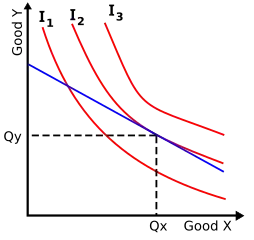
Why is it usually required that utility function be concave? Is it because concavity is a necessary (or sufficient?) assumption for a unique equilibrium?

Can someone please spell this out for me? Thank you. Edit: To clarify, I'm interested in the mathematical (modeling) reason for concavity. That concavity implies diminishing marginal utility and risk aversion is another matter.

Adam Bailey
  • 8,354
  • 1
  • 21
  • 36
Ohad Osterreicher
  • 125
  • 1
  • 6
  • 3
    In contexts with uncertainty, you can also connect concavity to risk aversion. – Bayesian Aug 01 '21 at 19:28
  • 1
    I feel for me 'concavity' captures the spirit of a trade-off in economics. But yes, in terms of modelling, concave programming ensures a maximum. – EB3112 Aug 01 '21 at 20:41
  • 2
    I've taken the liberty of editing the title of your question to reflect what I understand you are asking. Please feel free to reverse my edit if I've misunderstood. – Adam Bailey Aug 02 '21 at 18:54

2 Answers2

14

I disagree with @bbecon. I agree with @bbecon that concave utility functions present nice mathematical properties which help theorists develop analytical models.

If the OP's question was why utility functions are concave, the fundamental argument is that utility experiences diminishing returns.

Examine the image below, taken form here.

enter image description here

Let's say good X is coffee and good Y is cake. If you have 1 cup of coffee, getting a 2nd may increase your utility, but not by as much as the first one. Idem for 2 slices of cake. But if you could get 1 cup of coffee and 1 slice of cake, you would be most happy.

This argument fails under some special circumstances (e.g. this), but I think it's reasonable in most cases.

LBogaardt
  • 281
  • 1
  • 4
  • This coupled with risk aversion makes more sense to me than bbecon's answer. – Richard Hardy Aug 02 '21 at 09:55
  • @RichardHardy, risk aversion probably doesn't exist – crobar Aug 02 '21 at 11:16
  • 3
    @crobar that article was rather lacking in logic and reasoning. I kept waiting for it to get better, figuring it must with the link text you used. But it didn't... – Rick Aug 02 '21 at 14:04
  • @RichardHardy Classical risk aversion is the result of diminishing returns. It appears whenever the utility function is concave. It is not the reason why utility functions are concave. – LBogaardt Aug 02 '21 at 14:20
  • @Rick, if you want a more technical view try this article, most 'risk aversion' can be attributed to incorrectly considering ergodicity. More background in a nature paper here – crobar Aug 02 '21 at 14:22
  • 5
    @crobar, I think by now Peters (2019) can be safely considered ignorable. I got this impression from the rebuttal by Doctor et al. (2019) and reactions elsewhere. Basically, it seems an enthusiastic physicist discovered economics and though he can fix it quickly and easily; not much of a surprise given https://xkcd.com/793/. Just as unsurprisingly, his idea happens to be neither original nor very influential as it misses the target. But I am open to other perspectives (preferably with references). – Richard Hardy Aug 02 '21 at 15:07
  • 3
    @crobar, regarding Taleb, I have my reservations about his mastery of economics and finance. The fact that he refers to Peters (2019) just happens to make them stronger. – Richard Hardy Aug 02 '21 at 15:11
  • @RichardHardy, I guess this isn't the place for this debate, but Peters work is sound and backed by empirical evidence, see linked paper. Taleb is also correct, and has made a huge fortune in Finance by being correct. – crobar Aug 02 '21 at 15:34
  • 3
    @crobar, Peters' (and Meder et al.) work may be mathematically sound but it breaks in the applications to economic problems; some of his applications/examples are not valid, other not new. Try Doctor et al. (2019/2020) and especially their extended version / appendix (I have downloaded it but cannot find the source right now; should be possible to find from the paper itself) where all the details can be found. Perhaps your opinion of Peters (2019) will change after that. – Richard Hardy Aug 02 '21 at 15:59
  • Indeed, not the place for this debate. – LBogaardt Aug 02 '21 at 20:26
  • 3
    @crobar the idea is not sound, it is mathematically internally consistent but not applicable to economics. Geocentric model of solar system can also be mathematically made consistent and modeled if you willfully ignore wider research physics. – csilvia Aug 02 '21 at 23:08
  • 4
    @crobar, I have opened a new thread to continue the debate on a meta level (not on the level of maths but rather reactions of respected economists and possible consensus in the profession). Consider opening another one if you would like to discuss Peters' critique on the "direct" (non-meta) level; I would be curious to see what the community thinks about it. – Richard Hardy Aug 03 '21 at 07:13
  • 1
    @csilvia, I have opened a new thread to continue the debate on Peters' critique. – Richard Hardy Aug 03 '21 at 07:15
  • 1
    @LBogaardt, Classical risk aversion is the result of diminishing returns. Thanks for the comment. Took me a little while to think this through, but I guess you are right. – Richard Hardy Aug 03 '21 at 07:19
  • 1
    @RichardHardy If you liked xkcd's treatment of physicists, you may also enjoy this one from SMBC. – Giskard Aug 03 '21 at 10:22
7

More or less, yes.

Making the right assumption on the shape of the utility function allows you to prove existence or uniqueness of the equilibrium. The exact assumption you need depends on what exactly you are trying to prove and how general you want your result to be.

In the case of concavity, it also makes the equilibrium easier to find using the first-order conditions of the utility maximizer, because it makes sure that the local maximum that you find by setting the derivative of the Lagrangian to zero is also a global maximum.

bbecon
  • 688
  • 4
  • 9
  • Thank you very much! – Ohad Osterreicher Aug 01 '21 at 15:14
  • You're welcome. Glad to be of help – bbecon Aug 01 '21 at 20:18
  • 6
    -1 This may be correct as an explanation of why it can be convenient to assume that utility functions are concave. But as an explanation of why concave utility functions are usually concave it is surely wrong - for that we need evidence from behaviour, eg of diminishing marginal rates of substitution. – Adam Bailey Aug 02 '21 at 12:03
  • I believe my question was a bit misleading. I was interested in the mathematical reason why it is usually assumed that the utility function is concave. The issue of whether people actually have utility functions and what shape they are and why was not of my concern. – Ohad Osterreicher Aug 02 '21 at 12:18
  • 1
    @OhadOsterreicher That's fine. In that case, this is indeed the correct answer. Could you update your original question above to make that a bit more clear (for future readers)? – LBogaardt Aug 02 '21 at 14:21
  • 1
    Yes my interpretation of the question was "what does the concavity assumption buy you in practice", (he asked "why is it REQUIRED", which makes me think of a mathematical condition rather than an empirical property). Of course, that is a distinct question from whether concavity is a good assumption in the first place. One problem I have with LBogaardt comment is that utility functions express the same preferences up to a monotonic transformation. Ex: U=sqrt(xy) expresses the same (convex) preferences as U=(xy)^2, but the first utility is concave the latter convex.

    https://bit.ly/3C7Nhmb

     – bbecon Aug 02 '21 at 19:16