Seemingly simple consumer theory problem

Question

A function $v: \mathbb{R}^K_+ \xrightarrow{} \mathbb{R}_+$ is is said to be a valuation function if

1. The value of function $v$ at $x = \textbf{0}$ is $0$: $v(\textbf{0}) = 0$
2. $v$ is continuous on the domain $\mathbb{R}^K_+$, strictly increasing and strictly concave on $\mathbb{R}^K_{++}$
3. For any $p \in \mathbb{R}^K_{++}$, the set $A(p) = \{x \in \mathbb{R}^K_+| v(x) \geq p \cdot x\}$ is compact, the set $A^*(p) = A (p)-\{\bf{0}\}$ is nonempty and lies inside $\mathbb{R}^K_{++}$.

Show that a if $v$ is a valuation function, for every $p \in \mathbb{R}^K_{++}$, for every $x \in \mathbb{R}^K_{++}$, there exist $t>0$ small enough that $$ v(tx) > p\cdot tx $$

In other word, for every $p>\bf{0}$, if you zoom the set $A(p)$ sufficiently close at the origin, it contains all the points near the origin in first quadrant.

Remark 1: This is the problem I reduce from a microeconomics problem I am working on. I want to extend the Inada condition to multivariate case in a topological way. My prototype function is $f(x,y)=x^{\alpha}y^{\beta}$ where $\alpha+\beta <1, \alpha>0,\beta>0$. This family of functions satisfy (1),(2),(3) and the property I want to prove, say (4). I am trying to show either (1),(2),(3) => (4) or should I include (4) as an additional axiom?

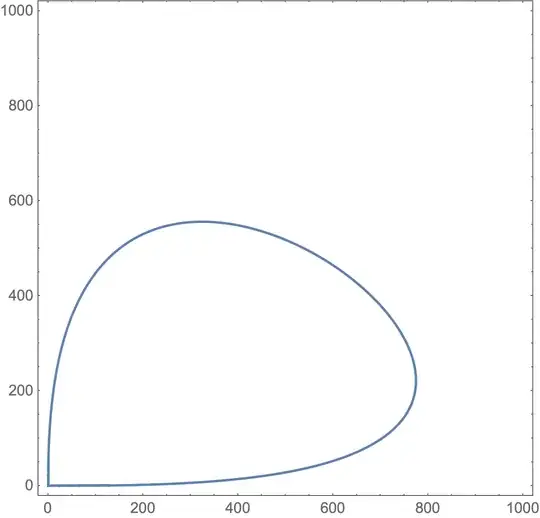
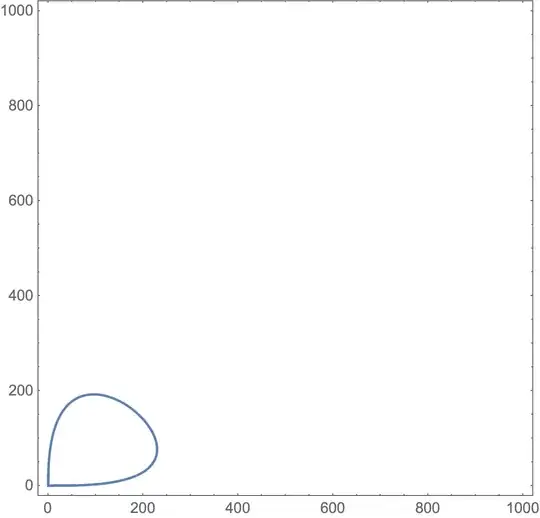
Remark 2: A few examples of $A(p)$

1. An example of A(p) when p is small

2. An example of A(p) when p is large

(4) is demonstrated by the geometric fact that the contours approach vertical and horizontal axis near $0$.

Answer 1

It follows indeed from the first three conditions, though I did not find a simple proof. Here is a messy one:

Observe first that, $v(tx)>p\cdot tx$ with $t>0$ is equivalent to $v(tx)/t>px$. By replacing $p$ by some multiple, we can see that the right-side can take any value without changing the left value. The function $t\mapsto v(tx)$ is strictly concave, strictly increasing, and has value $0$ at $0$. The problem is then equivalent to showing that its right derivative is infinite for all $x\gg 0$. That the right derivative exists follows from the concavity of $v$.

As it turns out, it is enough to find a single $x^*\gg0$ such that $t\mapsto v(tx^*)$ has an infinite right derivative at $0$.

To see this, let $x\gg 0$. There is some $\delta>0$ such that $x\gg \delta x^*$. Take some $K>0$. For $t>0$ small enough, we have $v\big(\delta t~x^*\big)/(\delta t)>K/\delta $ or $v(\delta t x^*)/t>K.$ Since $v$ is strictly increasing on the interior, $v(tx)/t>v(t\delta x^*)/t>K$ for $t>0$ small enough. Therefore, the function $t\mapsto v(tx)$ must have infinite right derivative at $0$.

It remains to find the damn $x^*$. Let $\Delta$ be the $K-1$-dimensional unit simplex. For each $N$, there must exist some $x\in\Delta$ such that the function $t\mapsto v(tx)$ has a right derivative of at least $N$ at $0$. Otherwise, for $p=(N,N,\ldots,N)$ we would have $A(p)-\{0\}=\emptyset.$ Also, $A(p)-\{0\}\subseteq\mathbb{R}^K_{++}$ implies that such an $x$ must be positive in each coordinate. So let $x_n\in\Delta$ be such that $t\mapsto v(tx_n)$ has a right derivative of at least $n$ at $0$. Now let $$x^*=\sum_{i=1}^\infty\frac{1}{2^i}x_{2^i}.$$ That the relevant series converges follows from any norm being bounded on the compact set $\Delta$ and absolute convergence implying convergence. Clearly, $x^*\gg 0$ since $x_{2^i}\gg 0$ for all $i$. It remains to show that $t\mapsto v(tx^*)$ has an infinite right derivative at $0$. Since $$t^{-1}~v\bigg(t\sum_{i=1}^\infty\frac{1}{2^i}x_{2^i}\bigg)>t^{-1}~v\bigg(t\sum_{i=1}^n\frac{1}{2^i}x_{2^i}\bigg)$$ for all $n$ by $v$ being strictly increasing on the interior, it suffices to show that for each $K>0$, there exists some $n$ such that $$t^{-1}~v\bigg(t\sum_{i=1}^n\frac{1}{2^i}x_{2^i}\bigg)>K$$ for $t>0$ small enough. Let $S_n=\big(\sum_{i=1}^n 1/2^i\big)^{-1}$ and note that $$t^{-1}v\bigg(tS_n\sum_{i=1}^n\frac{1}{2^i}x_{2^i}\bigg)=t^{-1}v\bigg(\sum_{i=1}^n S_n\frac{1}{2^i}t x_{2^i}\bigg)\geq\sum_{i=1}^n S_n\frac{1}{2^i}t^{-1}v(tx_{2^i})$$ by the concavity of $v$. Since $\lim_{t\downarrow 0}t^{-1}v(t x_{2^i})\geq 2^i$, this sum is almost $S_n n$ for $t>0$ small enough. Now $S_n$ converges to $1$, so $S_n n$ is larger than $K$ for $n$ large enough and $t>0$ small enough.