6

I always face a dilemma on whether to assume prices to have a time trend or not while modelling. It is also partly a statistics problem. Let me explain. Assume I have time series, $y_t$ of price of a commodity which on plotting appears to be having an upward slope (which is after all true for majority of items).

When I apply unit root test without drift, the result is non-rejection of unit root. However, if I include a drift term, the result is rejection of unit root.

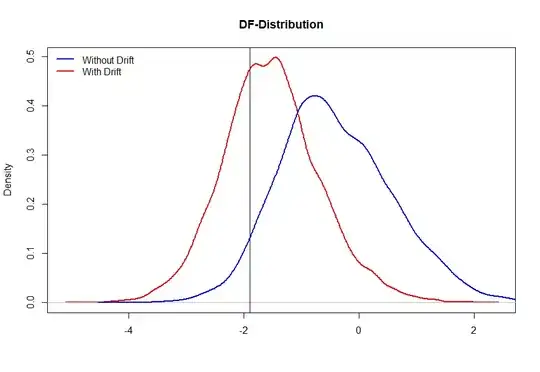
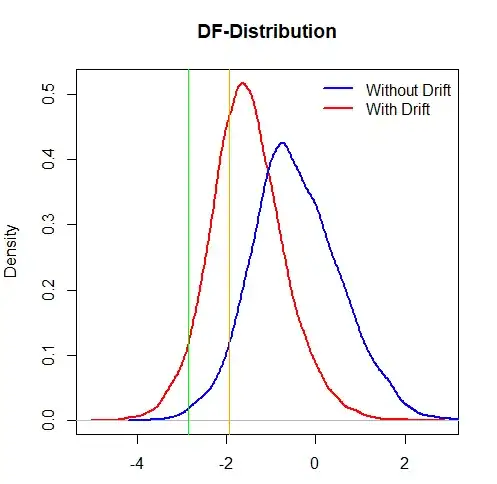
Now, if the true process is random walk without drift, inclusion of drift is very likely to incorrectly reject the null (below is a simulation study that shows that if the true process is pure random walk, inclusion of drift rejects the null around 34% of times). The red-line is the distribution of t-statistic when ADF test is applied with drift, and blue-line when applied without drift (which is the true process).

enter image description here

(the vertical line is the 0.05 quantile value for DF-distribution - blue curve)

Now if the series did have a time trend (without unit root), ADF test (without drift) almost never rejects the null of unit root.

Hence the dilemma. My take is that the answer (whether trend is stochastic or deterministic) has to come from theory. So the question boils down to Why should prices have a deterministic trend? What economic dynamics would justify modelling the series as, say AR(1) process with time trend?

Code:

'%>%'=magrittr::'%>%'
n=1e4
tt_coef = 0.1

ar1 = function(phi, n=1000, tt=0, tt_coef=0,sd) {
  y = numeric(1000+100)
  for (i in 2:length(y)) {
    y[i] = phiy[i-1] + tttt_coef*i + rnorm(1,mean = 0, sd = 1)
    }
  return(tail(y,n)) # first 100 observations burned to remove impact of initial condtns
}


samples_tt = replicate(n,ar1(phi = 0.7,tt = 1, tt_coef = tt_coef, sd = 8),simplify = F)
df_stats_tt = lapply(samples_tt, function(x) urca::ur.df(x,lags = 0,
                                                         type = 'none')@teststat) %>%
  unlist()


samples_rw = replicate(n,ar1(phi = 1, sd = 1),simplify = F)
df_stats_rw = lapply(samples_rw, function(x) urca::ur.df(x,lags = 0,
                                                         type = 'none')@teststat) %>%
  unlist()


df_stats_drift = lapply(samples_rw, function(x) urca::ur.df(x,lags = 0,
                                                            type = 'drift')@teststat[,1]) %>%
  unlist()


sum(df_stats_drift<quantile(df_stats_rw, probs = 0.05))/n
sum(df_stats_tt < quantile(df_stats_rw, probs = 0.05))/n


plot(density(df_stats_drift), type = 'l', lwd = 2, 
     col = 'red', main = 'DF-Distribution', xlab = '')
lines(density(df_stats_rw), type = 'l', lwd = 2, col = 'blue')
abline(v = quantile(df_stats_rw, prob = 0.05))
legend('topleft', legend = c('Without Drift', 'With Drift'), 
       col = c('blue', 'red'), lwd = 2, bty = 'n')
Dayne
  • 1,725
  • 6
  • 18
  • +1, I overall think it is a interesting question but it could be still improved if you would first attempt to look at the literature for the solution/partial solution and build the question on that. – 1muflon1 Mar 07 '21 at 09:40
  • 1
    @1muflon1: I have tried to do that and in what I could find is that most of the time prices are modelled as random walk (without drift). But then there are papers which (without giving economic justification) allow for drift term - for example by adding an intercept term in ECM. – Dayne Mar 07 '21 at 09:44
  • 2
    sometimes even if books/papers do not offer solution it is good if you mention you had look at them because then people know what you already know or what other arguments you looked at but found unconvincing. It will help them to give you better answer – 1muflon1 Mar 07 '21 at 09:46

1 Answers1

2

Should Prices (or Price Indices) be modelled with deterministic trend?

Often yes. Prices could have time trend for various reasons. For example, the most obvious one is inflation. While inflation is the increase in aggregate prices not necessary in every individual one, aggregate price level would not increase if significant number of prices would not. Thus you would expect prices to have upward time trend in many prices in any country experiencing inflation. For this reason when people analyze CPI they typically test unit root hypothesis against trend stationary (often even with non-linear trends like in Bierens 1997)

The CPI logic might not be applicable to every single individual price, some of them might happen to be stable, but it can be extended to many individual prices.

The rationale for trend in CPI is simply that central banks target increase in CPI, so you would expect it to have positive trend because based on economic theory central banks are able to control (with more or less precision) inflation (see various rigorous models of this in Romer Advanced Macroeconomics). If on the other hand central banks would target $0\%$ inflation you would not want to include the trend.

Edit: In response to question about inclusion of drift term where there is no trend it does not lead to bias in general. To explain this consider the Dickey-Fuller test and its mechanics:

The DF test with drift is given as:

$$\Delta Y_t = \delta + (\theta-1) Y_{t-1} +\epsilon$$

Now this is at its hart estimated just by OLS. Consequently, if the model is supposed to have drift but you exclude it and estimate $$\Delta Y_t = (\theta-1) Y_{t-1} +\epsilon$$ you will bias your estimation of $(\theta-1)$, but the converse will not hold. If you estimate $\Delta Y_t = \delta + (\theta-1) Y_{t-1} +\epsilon$ but series has no drift then in expectations $\delta$ will just be zero and estimation of $(\theta-1)$ will not be biased. This is crucial because even though we do not care about $(\theta-1)$ per se but about value of the DF test, if $(\theta-1)$ is estimated in a biased manner any subsequent DF statistics is useless (also note running auxiliary DF test and examining if $\delta$ is significant and close to zero or not is cheap way of quickly assessing if it is important).

Now when it comes to $t$ values from DF test you have to realize that you are not using critical values based of DF distribution. Under the null the DF test distribution is non-standard so appropriate critical values have to be tabulated using Monte-Carlo simulations for the non-standard distribution that holds under the null (see Verbeek, A Guide to Modern Econometrics. pp 292).

The correct critical values for DF test with trend and with drift are given in the table below (from ibid).

enter image description here

The table does not include appropriate value for specification with no drift but I found that here.

You will note if you apply these appropriate critical values to the distribution of $t$-statistics of DF test from your simulations you will find that areas in the tail are virtually identical between the DF test with and without drift. The area left of green line $t^* = -2.87$ below red dist. is very close to the area left of orange line $t^*=−1.942$ below blue dist*.

The areas wont be exactly same of course, and using DF test with drift will in marginal cases lead to incorrect inferences, so you are right into being interested in theoretical reasons for whether there should be drift or no if you want to be pedantic about it (which you should - don't get me wrong). However, this being said, whenever in doubt you should use DF with drift, because excluding it might lead to bias in $\theta-1$ itself and at that point any inferences are completely useless and it is not possible to even get right $t$-stat since $DF_t= \frac{\hat{\theta}-1}{se(\hat{\theta})}$ - if you get numerator wrong then that is the end.

enter image description here

*: note I modified the code to have only 500 observations so I can apply appropriate critical values. In addition, I change the series to be just random walk because there is no qualm that non-drift version is wrong if there is a drift.

1muflon1
  • 56,292
  • 4
  • 53
  • 108
  • I think I wasn't clear enough in my question. (1) the fact that random walk process doesn't necessarily has an upward slope, is actually a motivation of this question. Given that most prices have an upward slope - modelling them as random walk without drift seemed a little uncomfortable (as they seem to be representing only a subset of possibilities). – Dayne Mar 07 '21 at 11:11
  • (2) Your example of that price can be modelled is cumulative sum of past errors is just assuming it to be random walk without drift. The problem is I am looking for economic justification of also including a time trend in that equation. – Dayne Mar 07 '21 at 11:13
  • @Dayne you can have random walk with a time trend (here that would be the changes in price due to shocks + trend caused by inflation). I will edit that in my answer but you should edit, your question - also this is an example why some evidence of prior search would help as that would clarify your question right away – 1muflon1 Mar 07 '21 at 11:13
  • (3) The economic justification of the argument that time trend can be because of inflation is exactly what I am looking for. If an item has a time trend because of inflation, then it makes the argument circular as what would explain a time trend in the index? – Dayne Mar 07 '21 at 11:16
  • @Dayne it is not circular argument, explanation in the time trend in the index is simply that central banks choose to pursue slightly inflationary policy instead of maintaining perfect price stability. – 1muflon1 Mar 07 '21 at 11:18
  • Precisely, I can use it as a counter-argument. Since the time trend in index is because of policy of the bank, it is not actually time trend. For example, central bank's policy can be taken as a random shock (for example at some point they may decide to raise rates enough to make index drop (inflation can still be positive) - thereby going against the 'time' trend of the index. – Dayne Mar 07 '21 at 11:21
  • I have edited the question and emphasized the main doubt. – Dayne Mar 07 '21 at 11:23
  • @Dayne they could do that but empirically they have inflation bias so if you want to test for unit root in the price level you have to account for that. Also central bank policy is not random so modelling it as random $N(0,1)$ process does not make sense, whatever policy they choose it is not random in a way macro shocks are central bank policy can be best modeled through some policy rule such as Taylor rule or some other rule for its behavior – 1muflon1 Mar 07 '21 at 11:27
  • I am not modelling bank policy as $N(0,1)$, I am just looking for a justification. Given that change in bank's policy rate can be positive also (although may be with lower probability), justifying a time trend is difficult. – Dayne Mar 07 '21 at 11:30
  • @Dayne it is not difficult 1.) you should include time trend in your empirical application if it is possible to detect it (there are tests for that regardless of any theoretical justification). 2. you cant say that just because something could happen that invalidates theoretical explanations for something happening. A monopolist with high market power facing inelastic demand could be always pricing its product at marginal cost but would you be surprised if no such monopolist would ever do something like that? It is general consensus that small level of inflation improves macro stability – 1muflon1 Mar 07 '21 at 11:39
  • central banks job is to maintain macro stability. Thus even if they could keep perfect price stability with inflation at 0 which would mean there would be no trend in prices, they wont do that because it goes against their objective (the same way as monopolist could price goods at P=MC but it would fail to maximize profit in the case with market power and inelastic demand). – 1muflon1 Mar 07 '21 at 11:40
  • Sorry, as I said motivation of my question is to get a deep economic logic. The argument that it may be possible to detect has a major issue. Given an upward sloping time series, suppose a unit root test may give result that: (1) it is random walk without drift; (2) it is stationary with drift. Now how do you decide whether to take time trend or not? – Dayne Mar 07 '21 at 11:48
  • @Dayne but what is your definition of deep economic reasoning? For example, economic theory tells us that prices are given by demand and supply which depend on peoples preferences. But that does not mean that prices could be chosen by market in a way demand does not equal supply. Anything could happen. Analogously, central bank could do anything but due to its mandate and targets it will have bias toward inflation. Central banks explicitly say they target $\approx 2%$ increase in CPI per year (you can view this as their underlaying preferences), how deeper can we go? – 1muflon1 Mar 07 '21 at 12:00
  • also note an important fact about unit root testing. Inclusion of time trend when it is not necessary does not bias the estimation only omission if necessary does. This is the same as with any regression. Omission of relevant variables causes bias, inclusion of irrelevant ones only decreases efficiency. This is not to say that efficiency would not matter or could not lead to wrong inference, but when in doubt, regardless of theory it is best to try to test for presence of linear or non-linear trend in data – 1muflon1 Mar 07 '21 at 12:04
  • Thanks for valuable comments. Your last statement is actually not correct. I have added some simulation results in the question for clarity. – Dayne Mar 07 '21 at 13:14
  • @Dayne the new edit of your answer is interesting, it is possible I was mistaken there, could you please provide code for that result I would like to double check it myself – 1muflon1 Mar 07 '21 at 13:25
  • 1
    sure. I'll add the code below the question. – Dayne Mar 07 '21 at 13:28
  • @Dayne I edited my answer, actually I dont think I was wrong I provided some reasons for that. I also edited the first part based on your feedback – 1muflon1 Mar 07 '21 at 15:22
  • thanks for edits. So I am very well aware that t-statistic has non-standard distribution. That's why I did simulations to generate the critical values. Two, could you provide some good references on the statement that including $\delta$ in ADF regression will not make the estimate of $\theta-1$ biased under the null of unit root. – Dayne Mar 07 '21 at 16:14
  • (2) the critical values you have reported are with trend and without trend? ADF test has three settings: no drift, with drift, with drift and trend. I think the table has last two types. If so, then it is incorrect as critical values for pure random walk would be different. – Dayne Mar 07 '21 at 16:19
  • @Dayne you are welcome. 1. I don't have reference for that for particularly DF but I can give you reference for that for regression generally. DF is in the end just regression. But, Verbeek cautions against too restrictive DF as it can lead to bias and in footnote (pp 294) says: "if the mean of the series is known to be zero, the intercept term may be dropped from the regression, leading to a third variant of the Dickey-Fuller. This test is rarely used in practice. " From my experience in macro people often ignore the non-drift specification arguing it is better to relax restrictions – 1muflon1 Mar 07 '21 at 16:29
  • @Dayne 2. That is very good question, I am not sure Verbeek reports that table under text where he mentions only drift and no drift specification, he introduces specification with linear deterministic trend $\beta t$ later in the chapter and he calls in text specification with drift, model with deterministic trend. So I assume that is what the table is for. Regardless, if I recall correctly from my econometrics classes the DF critical values will always change when you change specification. Critical values should not be equal between specification with or without drift – 1muflon1 Mar 07 '21 at 16:33
  • If the mean of the series is known to be zero... this doesn't sound helpful. Random walk's mean is problematic. The initial condition decides the mean and it's impact is lost after enough observations. Note that the intercept term (drift) in DF regression means a time trend in level series. – Dayne Mar 07 '21 at 16:40
  • @Dayne by the way I am getting automated flags from the system that there are too many comments - we can continue in chat – 1muflon1 Mar 07 '21 at 16:40
  • Let us continue this discussion in chat. – 1muflon1 Mar 07 '21 at 16:40
  • @Dayne: I didn't read all the comments If you need to model prices, you're better off modelling returns and then converting back to prices afterwards. Prices are extremely difficult to model because they are non-stationary in wacky non-constant ways. returns have much nicer properties. – mark leeds Mar 08 '21 at 01:31