I've been reading about prospect theory lately and have read often that prospect theory predicts people will be risk averse in gains and risk seeking in losses. This statement is typically supplemented with the phrase ", contrary to the standard expected utility theory model".
However, I'm not sure how expected utility theory deals with losses. Is it that EU theory assumes people who are risk averse in gains will be risk averse in losses as well? If so, how do you model this mathematically?
If our risk-averse EU maximizer has $u(x)=\sqrt{x}$ for $x>=0$, would the equivalent function in losses be $u(x) = -x^2$ for $x<0$? If so, wouldn't that mean that they are overweighting the loss component relative to the gain component - which is not an element of expected utility theory.
Graphically, a prospect theory value function is typically drawn as 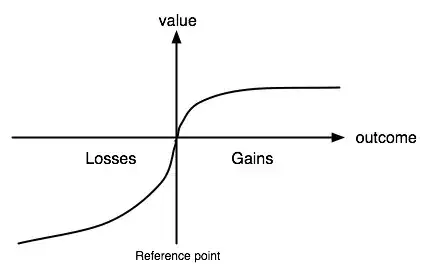 .
.
How would you draw the equivalent graph for an expected utility theory value function?