Why stochastic dominance is "stochastic"?

Question

I think the CDF is pretty much fixed, so the FOSD (first order stochastic dominance) is pretty much non-stochastic. Why does it have a "stochastic" in its name?

Answer 1

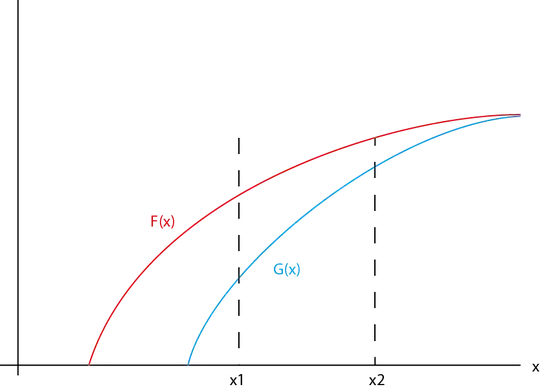
In the below figure, CDF $F(\cdot)$ is first-order stochastically dominated by $G(\cdot)$. But $X_1$ and $X_2$ fall within the support of both distributions. So it would be possible to draw $X_1$ from $F$ and $X_2$ from $G$, or to draw $X_2$ from $F$ and $X_1$ from $G$.

More generally, if $X_G$ is a draw from $G$ and $X_F$ is a draw from $F$ then $X_F-X_G$ will sometimes be positive and sometimes negative. In this sense, the dominance is only stochastic: $G$ produces larger draws than $F$ on average, but not all of the time.