I think there are two legitimate sources of complaint. For the first, I will give you the anti-poem that I wrote in complaint against both economists and poets. A poem, of course, packs meaning and emotion into pregnant words and phrases. An anti-poem removes all feeling and sterilizes the words so that they are clear. The fact that most English speaking humans cannot read this assures economists of continued employment. You cannot say that economists are not bright.
Live Long and Prosper-An Anti-Poem
May you be denoted as $k\in{I},I\in\mathbb{N}$, such that $I=1\dots{i}\dots{k}\dots{Z}$
where $Z$ denotes the most recently born human.
$\exists$ a fuzzy set $Y=\{y^i:\text{Human Mortality Expectations}\mapsto{y^i},\forall{i\in{I}}\},$
may $y^k\in\Omega,\Omega\in{Y}$ and $\Omega$ is denoted as "long"
and may $U(c)$, where c is the matrix of goods and services across your lifetime
$U$ is a function of $c$, where preferences are well-defined and $U$ is qualitative satisfaction,
be maximized $\forall{t}$, $t$ denoting time, subject to
$w^k=f'_t(L_t),$ where $f$ is your production function across time
and $L$ is the time vector of your amount of work,
and further subject to $w^i_tL^i_t+s^i_{t-1}=P_t^{'}c_t^i+s^i_t,\forall{i}$
where $P$ is the vector of prices and $s$ is a measure of personal savings across time.
May $\dot{f}\gg{0}.$
Let $W$ be the set $W=\{w^i_t:\forall{i,t}\text{ ranked ordinally}\}$
Let $Q$ be the fuzzy subset of $W$ such that $Q$ is denoted "high".
Let $w_t^k\in{Q},\forall{t}$
The second is mentioned above, which is the misuse of math and statistical methods. I would both agree and disagree with the critics on this. I believe that most economists are not aware of how fragile some statistical methods can be. To provide an example, I did a seminar for the students in the math club as to how your probability axioms can completely determine the interpretation of an experiment.
I proved using real data that newborn babies will float out of their cribs unless nurses swaddle them. Indeed, using two different axiomatizations of probability, I had babies clearly floating away and obviously sleeping soundly and securely in their cribs. It wasn't the data that determined the result; it was axioms in use.
Now any statistician would clearly point out that I was abusing the method, except that I was abusing the method in a manner that is normal in the sciences. I didn't actually break any rules, I just followed a set of rules to their logical conclusion in a way that people do not consider because babies don't float. You can get significance under one set of rules and no effect at all under another. Economics is especially sensitive to this type of problem.
I do belive that there is an error of thought in the Austrian school and maybe the Marxist about the use of statistics in economics that I believe is based on a statistical illusion. I am hoping to publish a paper on a serious math problem in econometrics that nobody has seemed to notice before and I think it is related to the illusion.
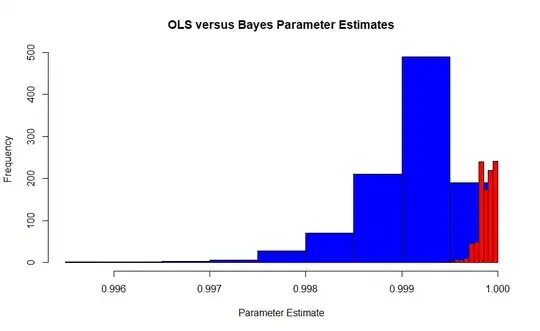
This image is the sampling distribution of Edgeworth's Maximum Likelihood estimator under Fisher's interpretation (blue) versus the sampling distribution of the Bayesian maximum a posteriori estimator (red) with a flat prior. It comes from a simulation of 1000 trials each with 10,000 observations, so they should converge. The true value is approximately .99986. Since the MLE is also the OLS estimator in the case, it is also Pearson and Neyman's MVUE.
Note how relatively inaccurate the Frequency based estimator is compared to the Bayesian. Indeed, the relative efficiency of $\hat{\beta}$ under the two methods is 20:1. Although Leonard Jimmie Savage was certainly alive when the Austrian school left statistical methods behind, the computational ability to use them didn't exist. The first element of the illusion is inaccuracy.
The second part can better be seen with a kernel density estimate of the same graph. 
In the region of the true value, there are almost no examples of the maximum likelihood estimator being observed, while the Bayesian maximum a posteriori estimator closely covers .999863. In fact, the average of the Bayesian estimators is .99987 whereas the frequency based solution is .9990. Remember this is with 10,000,000 data points overall.
Frequency based estimators are averaged over the sample space. The missing implication is that it is unbiased, on average, over the entire space, but possibly biased for any specific value of $\theta$. You also see this with the binomial distribution. The effect is even greater on the intercept.

The red is the histogram of Frequentist estimates of the itercept, whose true value is zero, while the Bayesian is the spike in blue. The impact of these effects are worsened with small sample sizes because the large samples pull the estimator to the true value.
I think the Austrians were seeing results that were inaccurate and didn't always make logical sense. When you add data mining into the mix, I think they were rejecting the practice.
The reason I believe the Austrians are incorrect is that their most serious objections are solved by Leonard Jimmie Savage's personalistic statistics. Savages Foundations of Statistics fully covers their objections, but I think the split had effectively already happened and so the two have never really met up.
Bayesian methods are generative methods while Frequency methods are sampling based methods. While there are circumstances where it may be inefficient or less powerful, if a second moment exists in the data, then the t-test is always a valid test for hypotheses regarding the location of the population mean. You do not need to know how the data was created in the first place. You need not care. You only need to know that the central limit theorem holds.
Conversely, Bayesian methods depend entirely on how the data came into existence in the first place. For example, imagine you were watching English style auctions for a particular type of furniture. The high bids would follow a Gumbel distribution. The Bayesian solution for inference regarding the center of location would not use a t-test, but rather the joint posterior density of each of those observations with the Gumbel distribution as the likelihood function.
The Bayesian idea of a parameter is broader than the Frequentist and can accomodate completely subjective constructions. As an example, Ben Roethlisberger of the Pittsburgh Steelers could be considered a parameter. He would also have parameters associated with him such as pass completion rates, but he could have a unique configuration and he would be a parameter in a sense similar to Frequentist model comparison methods. He might be thought of as a model.
The complexity rejection isn't valid under Savage's methodology and indeed cannot be. If there were no regularities in human behavior, it would be impossible to cross a street or take a test. Food would never be delivered. It may be the case, however, that "orthodox" statistical methods can give pathological results that have pushed some groups of economists away.



I find it very funny when an economist says something like that. Apparently it's perfectly acceptable to say people choose bundles of goods based on preferences and budget restrictions but god forbid writing the same idea as a constrained optimization problem.
– Pedro Cavalcante Dec 10 '18 at 07:27In all honesty, econ majors/grad students who just can't get that whatever logical statement which can be written in plain english can also be written as a mathematical statement - and writing it that way is better because now you prove theorems and do comparative statics in a more transparent way - are bound to be poor professionals and/or irrelevant researchers.
– Pedro Cavalcante Dec 10 '18 at 07:29