6

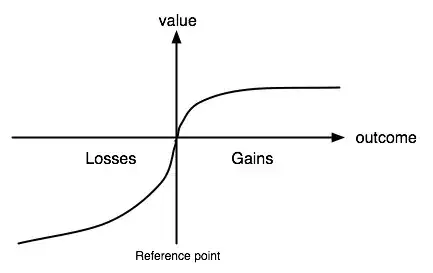
This is Kahneman's value-plot on prospect theory:

enter image description here

QUESTION: Why is the Marginal Utility of losses deminishing?

CONTEXT:

  • I fully understand that the Marginal Utility of gains deminishes: 100 dollar gains has less utility to me when I am rich than when I am poor.

  • But to me it is different with losses: If I can choose to lose 100 dollars for sure or a 50% chance to lose 200 dollars I would definitely not go for the bet! Why would I risk losing even more? After all, like most people, I am risk-averse. My reference point would be that I already lost 100 euro's.

  • Furthermore: If all I own should be 200 dollars, I might regret losing 100 dollars very much, but I will regret losing a second 100 dollars even more because then I would be left with nothing and I can't buy any food.

  • In other words: I guess my reference point is always zero and compared to that I will always be risk-averse... but isn't that what most people do or should do?

UPDATE: This article shows that the Value-curve can also be shaped differently, for example under time pressure: https://www.sciencedirect.com/science/article/pii/S0749597815000722

tripleee
  • 132
  • 7
GambitSquared
  • 161
  • 3

1 Answers1

4

The value function used in Kahneman's prospect theory (which your plot shows) is supposed to capture empirically observed behavior of people's attitudes towards gains/losses as well as to risks in those domains.

In the domain for gains, people are usually risk averse. However, in the domain for losses, people do tend to take larger risks. A nice illustration is the observation that when a gambler is losing money (relative to the amount he came to the casino with), he tends to wager on higher stakes (larger risks), perhaps in an attempt to "win back" the losses.

So the convex curvature in the domain of losses is meant to capture this type of behavior.

In fact, prospect theory's treatment of people's risk attitude is even more nuanced than the above. In addition to the S-shaped value function you showed, it also has a component that allows for non-linear probability weighting. Together, the value function and non-linear probability weighting generate the following four-fold classification of risk attitudes: \begin{array}{c|cc} &\text{gains}&\text{losses}\\\hline \text{low probability}&\text{risk loving}&\text{risk averse}\\ \text{high probability}&\text{risk averse}&\text{risk loving} \end{array}

See Kahneman and Tversky (1992) for more detail.

Herr K.
  • 15,409
  • 5
  • 28
  • 52
  • Doesn't your table imply that the shape of the value function depends on the quantity of the probabilities involved? – GambitSquared Mar 01 '18 at 00:08
  • 1
    @GambitSquared: Yes, it does. As I said, the value function and non-linear probability weighting generate the four-fold classification of risk attitudes. Prospect theory consists of both of these components. What you show in the question is only about the value function, which is only part of PT. – Herr K. Mar 01 '18 at 00:12
  • Furthermore the fact that this plot is supposed to be empirical doesn't connect it to my intuition and personal preference (see examples in my question). I just don't understand why someone would take such a bet. We aren't all addicted to gambling, are we? – GambitSquared Mar 01 '18 at 00:16
  • Would it be correct that the shape of the value function represents the high-probability case? What would the shape of the value function be in the low-probability case? – GambitSquared Mar 01 '18 at 00:19
  • 2
    @GambitSquared: The gambler's example in my answer is well-documented. I'm not making it up. Also, the paper linked at the end reports experimental evidence that a convex curvature in the domain of losses is justified. Regarding your last two questions: it may appear the way you're suggesting, but when the S-shaped value function and non-linear probability weighting are put together, it's hard to separate the effects of individual components, since the combo is highly non-linear. – Herr K. Mar 01 '18 at 00:27
  • This article shows that the Value-curve can also have a different shape in different circumstances. In this case the circumstance is time-pressure: https://www.sciencedirect.com/science/article/pii/S0749597815000722 – GambitSquared Mar 05 '18 at 12:10
  • @GambitSquared Sure. But how is this related to your original question, why the value function is convex over losses? If you have a different question, ask it in a different post. – Herr K. Mar 05 '18 at 12:17
  • Because it shows that the value-function over losses is not convex in all situations. – GambitSquared Mar 05 '18 at 12:19
  • @GambitSquared I don't dispute the finding you post. But your question was why utility over loss is convex. Also, your question suggested that you're interested in why Kahneman formulated the function as such. I addressed these two aspects in my answer. – Herr K. Mar 05 '18 at 12:36
  • As far as I understand it now, the answer to my question should be something like: "the marginal utililty of losses is not always diminishing, it depends on the situation, therefore the assumption in your question is wrong. The Value-plot can have a different shape such as in the situations you describe." Or something similar. Or am I missing something? – GambitSquared Mar 05 '18 at 12:42
  • @GambitSquared you're always welcome to post that as an answer – Herr K. Mar 05 '18 at 12:45
  • Of course, but since I am not an expert, I am not sure about the validity of that answer. It is just my tentative conclusion. – GambitSquared Mar 05 '18 at 12:48
  • Can you add a short explanation on what you meant by "low probability" and "high probability" in the table? – xuhdev Dec 01 '18 at 22:09
  • @xuhdev: "Low" and "high" are in reference to KT's original experiment. At the risk of quoting them out of context, think of "low probability" as "$p\le0.1$" and "high probability" as "$p\ge0.9$". But please, if you're really interested in this, read KT's paper linked in my answer. – Herr K. Dec 01 '18 at 22:26
  • @HerrK. Thanks, I'm just looking for a summary, but this has really confused me. Actually, what confused me is really what the probability means: The probability of what? – xuhdev Dec 02 '18 at 02:06
  • @xuhdev: probability of gains or losses – Herr K. Dec 02 '18 at 02:07