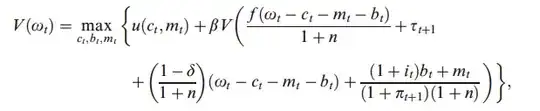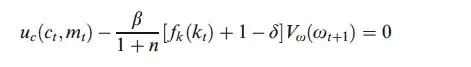I am reading Walsh's (2003) book on monetary economics. Specifically the chapter on money in utility function. I understand the basics of a value functions but I can't seem to get the same results as the author.
I.e the per capita budget constraint. He then finds an expression for $w_{t+1}$:
This is the first source of my confusion. Previously he defines output per worker as a function of capital per worker, i.e $y_{t}=f(\frac{k_{t-1}}{1+n})$ where $n$ is the population growth rate. But all of a sudden he changes it to $\frac{f(k_{t-1})}{1+n}$. I am aware that there are many typos in this book, is this just one of them or am I missing something trivial?
Either way, he uses the budget constraint to express $k_{t}$ as $w_{t}-c_{t}-m_{t}-b_{t}$ and the definition of $w_{t+1}$ to express the value function as:
Now, I don't know if it is because I am sleep deprived or because there is a typo, but I just can't seem to get the same results as Walsh. E.g, differentiating w.r.t $c_{t}$ I get:
$u_{c}(c_{t},m_{t}) + \beta*V_{w}(w_{t+1})[\frac{-f'(w_{t}-c_{t}-m_{t}-b_{t})}{1+n}(-1)+\frac{1+\delta}{1+n}(-1)]$
While Walsh gets
Am I missing something obvious or is there a typo?
Thanks in advance!