11

I am reading the paper 'The Structure of Urban Equilibria' by Jan Brueckner.

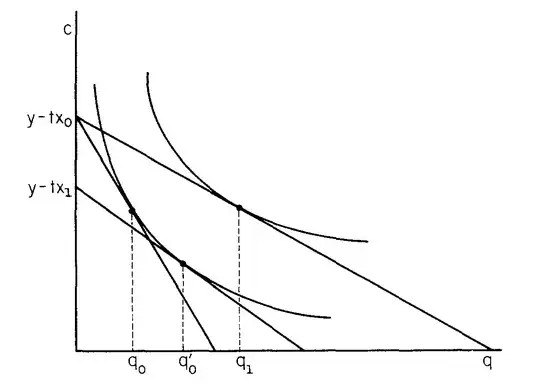
It uses a monocentric city model, where all consumers earn income $y$ at the centre of the city. They buy $q$ housing for a price $p$ at distance $x$ from the centre, incurring transport costs $tx$.

Consumers have a utility function:

$v(c,q)=v(y - tx - p(\phi)q(\phi),q(\phi))=u$

where $\phi=x,y,t,u$

The budget constraint is:

$c = y - tx - pq$

enter image description here

The tangency condition implies:

$\frac{v_1(y - tx - pq, q)}{v_2(y - tx - pq, q)} = p$

where the subscript 1 denotes partial differentiation w.r.t. the first argument etc.

The paper then discusses how $p$ and $q$ vary with $x, y, t$ and $u$.

If $\phi=x,y,t$, we stay on the same indifference curve. I find it relatively straightforward to find $\frac{\partial{p}}{\partial{x}},\frac{\partial{p}}{\partial{y}}$ and $\frac{\partial{p}}{\partial{t}}$.

If $\eta$ is the slope of the income-compensated demand curve, then $\frac{\partial{q}}{\partial{\phi}} = \eta\frac{\partial{p}}{\partial{\phi}}$.

Now to allow $u$ to vary. The budget constraint swings out to meet a new indifference curve, determining the new $p$ and $q$.

I can find $\frac{\partial{p}}{\partial{u}}$. Totally differentiate the utility function w.r.t u:

$\frac{d}{du}[v(y - tx - p(\phi)q(\phi),q(\phi))= u] = v_1(-\frac{\partial{p}}{\partial{u}}q-p\frac{\partial{q}}{\partial{u}})+v_2(\frac{\partial{q}}{\partial{u}})=1$

Since, by the tangency condition $v_2=pv_1$:

$v_1(-\frac{\partial{p}}{\partial{u}}q-p\frac{\partial{q}}{\partial{u}}+p\frac{\partial{q}}{\partial{u}})=v_1(-\frac{\partial{p}}{\partial{u}}q)=1$

So $\frac{\partial{p}}{\partial{u}} = \frac{-1}{qv_1}$.

The paper then quotes:

$\frac{\partial{q}}{\partial{u}} = [\frac{\partial{p}}{\partial{u}}-\frac{\partial{MRS}}{\partial{c}}\frac{1}{v_1}]\eta$

I don't know how to derive this. I'm guessing the first term in the square brackets is a substitution effect and the second term is an income effect.

Please help me understand this last expression $\frac{\partial{q}}{\partial{u}} = [\frac{\partial{p}}{\partial{u}}-\frac{\partial{MRS}}{\partial{c}}\frac{1}{v_1}]\eta$ and how to derive it.

StevenRJClarke1985
  • 423
  • 3
  • 8
  • 1
    What does $\dfrac{\partial p}{\partial u}$ represent? Isn't $p$ the (fixed) price of housing? Relatedly, is $x$ a choice variable or is it fixed? – Oliv Apr 04 '17 at 17:23
  • 1
    Also, what is $\dfrac{\partial q}{\partial \phi}$ given that $\phi$ is a three-dimensional vector? – Oliv Apr 04 '17 at 17:25
  • @Oliv. $p$ is the price of housing, and the slope of the budget constraint. If you look at the indifference curve above, the slope (and hence price) changes if you vary $x$ (distance from centre), $y$ (wage), $t$ (transport cost per unit distance) or $u$ (the utility that every one has - there is a spatial equilibrium in the city). $\frac{\partial{p}}{\partial{u}}$ then is the rate of change of price with utility. As you move to a higher utility indifference curve, the budget constraint pivots out to meet it, reducing in slope (hence price). – StevenRJClarke1985 Apr 04 '17 at 19:37
  • 1
    @Oliv. $\phi$ is not a vector. It can be $x, y, t$ or $u$, depending on which relationship you are interested in finding. So $\frac{\partial{q}}{\partial{x}}$ would be the rate of change of the amount of housing bought as you go further from the city centre, holding income, transport costs per unit distance and utility constant. $\frac{\partial{q}}{\partial{u}}$ would be the rate of change of the amount of housing bought as you increase the utility of all consumers, holding income, distance from centre and transport costs per unit distance constant. – StevenRJClarke1985 Apr 04 '17 at 19:40
  • dont have enough rep to comment; just a student trying to help the answer along: ∂MRS/∂c = ∂u/∂q∂c then: I believe you're correct in your assumption that the first term is substitution effect the rate of change of the amount of housing bought = (∂p/∂u - [(v1)∂u/∂q∂c]) * income effect – scott Apr 04 '17 at 20:08

1 Answers1

6

The utility function under consideration is $v(c,q)$ and then

$$MRS(c,q) = \frac{\partial v/\partial q}{\partial v/\partial c} = v_2/v_1$$

make the functional denpendency of on $u$ explicit then you have

$$\frac{\partial}{\partial u}MRS(c(u),q(u)) = \frac{\partial MRS(c(u),q(u))}{\partial c} \frac{\partial c(u)}{\partial u} + \frac{\partial MRS(c(u),q(u))}{\partial q} \frac{\partial q(u)}{\partial u} = \frac{\partial p(u)}{\partial u},$$

where the last identity follows because you know that $p = MRS$. Now simply rearrange the identity

$$\frac{\partial MRS(c(u),q(u))}{\partial c} \frac{\partial c(u)}{\partial u} + \frac{\partial MRS(c(u),q(u))}{\partial q} \frac{\partial q(u)}{\partial u} = \frac{\partial p(u)}{\partial u},$$

to get

$$ \frac{\partial q(u)}{\partial u} = \frac{\left[\frac{\partial p(u)}{\partial u} - \frac{\partial MRS(c(u),q(u))}{\partial c} \frac{\partial c(u)}{\partial u}\right]}{\frac{\partial MRS(c(u),q(u))}{\partial q} },$$

then use that Brueckner has defined $\eta := \left[\frac{\partial MRS(c(u),q(u))}{\partial q}\right]^{-1}$ in footnote(3) to get

$$ \frac{\partial q(u)}{\partial u} = \left[\frac{\partial p(u)}{\partial u} - \frac{\partial MRS(c(u),q(u))}{\partial c} \frac{\partial c(u)}{\partial u}\right] \eta ,$$

and finally apply the rule that $\frac{\partial c(u)}{\partial u} = \frac{1}{\partial v/\partial c} = 1/v_1$ to get

$$ \frac{\partial q(u)}{\partial u} = \left[\frac{\partial p(u)}{\partial u} - \frac{\partial MRS(c(u),q(u))}{\partial c} \frac{1}{v_1}\right] \eta.$$

Jesper Hybel
  • 3,316
  • 12
  • 36