6

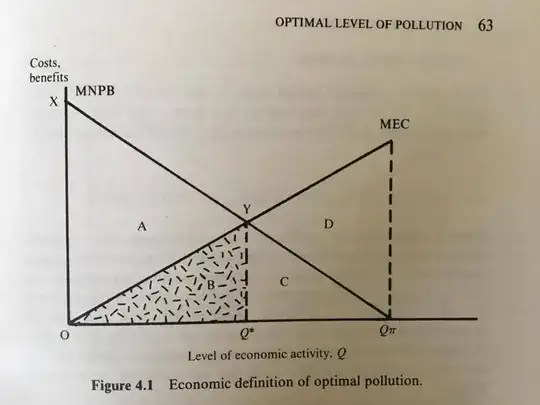
I'm reading the book "Economics of natural ressources and the environment" written by D. Pearce and R. Turner. They explain that the competitive equilibrium is not a Pareto optimum in case of (positive or negative) externalities. The example they use is a firm that has an activity Q and this activity creates some pollution. They illustrate it in figure 4.1 (figure below). MNPB stands for "marginal net private benefits" and MEC "marginal external cost". MEC is thus the extra damage done by pollution arising from the activity measured by Q.

The firm will try to maximize its benefit, i.e. reach an activity of Q$^\pi$. Q$^*$ is the level of activity to have a social optimum. I understand the reasoning so far.

What I do not understand is why Q$^\pi$ is not Pareto optimum. If we had to reach Q$^*$ from Q$^\pi$, the firm would loose some of its utility so Q$^\pi$ should be Pareto optimal.

I feel like I do not understand the exact meaning behind the notion of the Pareto optimality.

hello

Source of image: "Economics of natural ressources and the environment", D. Pearce and R. Turner, Harvester, New York, 1990.

EconJohn
  • 8,345
  • 6
  • 30
  • 64
Dust009
  • 163
  • 1
  • 4
  • I think there are a bunch of related questions on this site. Look http://economics.stackexchange.com/questions/3178/pareto-optimality-and-externalities?rq=1 or http://economics.stackexchange.com/questions/3116/converting-word-definitions-of-pareto-optimal-into-math-symbols?rq=1 – PhDing Jan 02 '17 at 15:16

2 Answers2

5

I feel like I do not understand the exact meaning behind the notion of the Pareto optimality.

It's not you. There are different senses of the phrase "Pareto Optimal," and you have to figure out from context which one is being used. The dictionary definition of Pareto Optimal is something like "An allocation from which any feasible change which makes any agent better off makes at least one agent worse off." The word to keep your eye on is "feasible."

In particular, it makes a big difference whether or not you consider side-payments feasible. In your example, if it is impossible to make side payments from "society" (i.e. whomever is harmed externally by the production of the good) to the producer, then $Q^\pi$ is Pareto Optimal. Of course, with no side payments, every point between $0$ and $Q^\pi$ is Pareto Optimal.

Almost always, however, we implicitly assume that side payments are possible. In that case, the point $Q^\pi$ is not optimal. Why not? Well, we could move from $Q^\pi$ to $Q^*$. This would make the producer worse off by $C$ and "society" better off by $C+D$. Now, if it is feasible to make "society" pay the producer some amount between $C$ and $C+D$, then we can say that moving from $Q^\pi$ to $Q^*$ while compensating the producer at least $C$ at the expense of "society" makes everyone better off. The fact that you can move off of $Q^\pi$ while making everyone better off means that $Q^\pi$ is not optimal.

This actually leads into a common criticism of Pareto Optimality. Normally, we just assume side payments are feasible. In fact, you get so habituated to making the assumption that it becomes invisible to you. So, you start to think (for example) that "free trade is Pareto Optimal" is a good argument for free trade. And that's untrue. The necessary side-payments are probably not feasible and are not actually made in practice.

Bill
  • 231
  • 1
  • 4
  • I disagree with your answer. "Feasible" is meant to be understood in the physical sense, whether the total number of goods assigned are available / can be produced. It has nothing to do with the market mechanism, e.g. whether side payments are allowed. If were to understand Pareto-optimality within the context of the given market mechanism then monopolies and some other unpleasant things would become Pareto-optimal. The concept exists to illustrate that some mechanisms are not great. – Giskard Jan 02 '17 at 19:03
  • @denesp You're worried about the distinction between "always" and "almost always." Different strokes, I guess. On the unpleasantness front, "Bill owns everything" is a Pareto Optimal allocation (by your definition and mine). – Bill Jan 02 '17 at 20:00
  • I always make sure my students know "Bill owns everything" is PO because it highlights very nicely that PO is an efficiency concept not a fairness concept. I have no clue what you mean by your other remark as I have not used the word always or anything similar as far as I can tell. – Giskard Jan 03 '17 at 07:48
  • @denesp Ok, so when you say " 'Feasible' is meant to be understood in the physical sense," you don't mean "feasible" is always meant to be understood that way? Then what do you disagree with? – Bill Jan 03 '17 at 15:21
  • So that is where you see always. However I still do not see how that would be "almost always", that still makes no sense to me. – Giskard Jan 03 '17 at 20:49
  • The alternative space in social choice theory, for example, is abstract. There are just a bunch of feasible alternatives. In that case, it's pretty clear that feasible does not mean feasible in the sense of not violating production relationships. It means feasible in the sense of ways society actually could be organized, taking account of all constraints. Non-cooperative game theory often has payoffs measured in utils, and the strategy spaces frequently don't include side payments. In both cases, we can and do talk about PO outcomes/equilibria. So, I think "almost always" is right. – Bill Jan 04 '17 at 13:13
  • I don't think the concept of Pareto-optimality in these disciplines coincides in all circumstances. Sorry but I still disagree with your answer. – Giskard Jan 04 '17 at 14:54
  • coincides with what? – Bill Jan 04 '17 at 15:32
  • The concept of PO in micro does not necessarily coincide with the concept of PO in social choice. – Giskard Jan 04 '17 at 17:31
  • OK, and how does the distinction "does not necessarily coincide / does necessarily coincide" differ from the distinction "almost always / always" Another way: I fail to see how your current position is even different from mine. We now agree that PO does not, in fact, always take "feasible" to mean not-violating-production-possibilities, right? – Bill Jan 04 '17 at 17:37
  • The question is clearly about microeconomics. In that context I do not agree. – Giskard Jan 04 '17 at 18:22
  • My problem is the one I outlined in my first comment. Would you say that a monopolistic market yields a Pareto-optimal outcome if the monopoly price is profit maximizing? Seems to me that this follows from your definition. But it also takes away a lot from the usefulness of Pareto-optimality when studying market mechanisms. – Giskard Jan 04 '17 at 18:46
  • Let us continue this discussion in chat. – Bill Jan 04 '17 at 18:56
1

This graph shows that the private sector will always be better of as $Q$ increases (but with a decreasing rate). Thus the question is up to which point the increase of $Q$ will not negatively affect the society.

Recall also that

Pareto improvement is defined to be a change to a different allocation that makes at least one individual better off without making any other individual worse off, given a certain initial allocation of goods among a set of individuals.An allocation is defined as "Pareto efficient" or "Pareto optimal" when no further Pareto improvements can be made.

That means that for any $Q$ in $(0,Q^*]$, private sector is better off and also society is better off since $MNPV>MEC$. However, for any $Q$ in $(Q^*,Q^π]$, the private sector improve its well-being but society is getting worst (since $MNPV<MEC$). That means that the point $Q^*$ is the pareto optimum

Yorgos
  • 189
  • 9