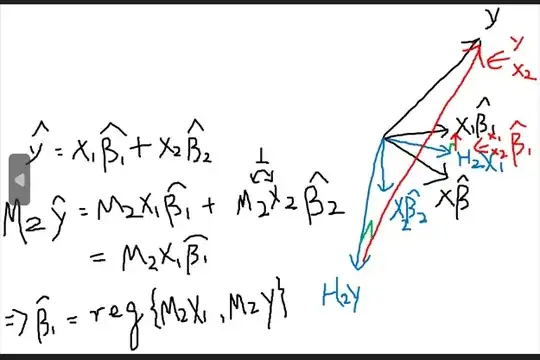
I have an equation of the form(all vectors): $y=X_1\beta_1+X_2\beta_2+u$.
I'm interested in knowing if the beta OLS estimators and respective residual for this equation are the same as for when we apply OLS to the following equations:
- $P_{X_1}y=P_{X_1}X_2\beta_2+v$
- $P_Xy=X_1\beta_1+X_2\beta_2+v$,
where the $P_Z$ are the usual definition of projection matrices, using $Z$.
So, I've tried using the FWL theorem, and I've got respectively:
- $\hat\beta_2 = (X_2' P_{X_1}X_2)^{-1}X_2'P_{X_1}y$, and $\hat v = (I- P_{X_1}X_2(X_2'P_{X_1}X_2)^{-1}X_2'P_{X_1})P_{X_1}y$. I was wondering if I miscalculated $\hat u$ since looking at equation 1, since both $y$ and $X_2\beta_2$ are projected in to the space spanned by columns of $X_1$, the residuals would be zero.
- $\hat\beta_2 = (X_2' M_{X_1}X_2)^{-1}X_2'M_{X_1}P_X y$, and $\hat v = (I- M_{X_1}X_2(X_2'M_{X_1}X_2)^{-1}X_2'M_{X_1})P_{X}y$. However, I do not see how the estimate for $\beta_2$ is equal in both cases, since if you notice that applying OLS to equation 2, we get $\hat \beta=(X'X)^{-1}X'P_X y=(X'X)^{-1}X'y$.
Any help would be appreciated.
Edit1: well, I found out how to do the 2nd point. We have to notice that $M_{X_1}P_X=(I-P_{X_1})P_X=P_X-P_{X_1}=P_X'-P_{X_1}'=(M_{X_1}P_X)'=P_X'M_{X_1}'=P_X M_{X_1}$ and that $ X_2'P_X=(P_X X_2)=X_2'$. As to the 1st point I have no idea...