In the morning, Google shows the temperature from four or five hours ago (around 2:00 a.m.). But then I update the report, and I get the temperature slightly lower than before.
Why is the temperature at 2:00 a.m. higher than the temperature at 7:00 a.m.?
The Earth is always radiating heat to the space. But in the day the Sun delivers some heat. The net heat flux is then defined as the sum of those two factors. If the energy delivered by the Sun is bigger than the cooling rate, the Earth is net warming (positive net flux – we can imagine it like heat is travelling "to us"), as opposed to the opposite case (cooling; negative net flux – heat is travelling "away").
In the day, the Sun warms the ground until the evening. The Sun's heating rate is higher than the cooling rate, so the temperature is rising until it gets to a point where the heating rate is same as cooling rate. This happens in the evening, so the temperature is steady at that point. But the Sun goes even lower, so the net flux becomes negative. In the night there is only cooling of Earth, so the temperature is falling steadily until the Sun is high enough that it balances the cooling. This happens at a point of a minimum temperature.
Of course, this is valid for most of the days, but we can have some other effects that can change the time of the minimum temperature (clouds, fronts or advection, for example).
On graph:
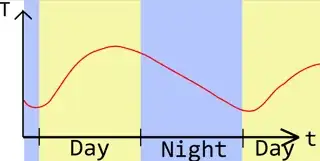
So, the temperature is falling over night after the sunset, but rises again after the sunrise. Thus, the temperature is at its lowest point in the morning.
Appendix for all you loving calculations:
Note: Simplified to toy model, no atmosphere
The cooling rate of the Earth is approximatelly given by the Stefan-Boltzmann equation:
$$j_E=\sigma\cdot T^4=5.670 \cdot 10^{-8} \frac{W}{m^2 K^4} \cdot (288.15 K)^4 = 390 \frac{W}{m^2}$$
The maximum heating rate of Sun in the zenith is $j_{\text{S max}}=1361 \frac{W}{m^2}$. So, the heating rate of Sun at altitude $\alpha$ is: $$j_S=j_{\text{S max}}\cdot \sin{\alpha}=1361 \frac{W}{m^2}\cdot \sin{\alpha}$$
When is the heating rate equal to zero?
$$0=j_S-j_E=1361 \frac{W}{m^2}\cdot \sin{\alpha} - 390 \frac{W}{m^2}$$ $$1361 \frac{W}{m^2}\cdot \sin{\alpha} = 390 \frac{W}{m^2}$$ $$\alpha = 17 °$$
So, with our calculations, the minimum temperature is at the time when the altitude is equal to 17°.
Your question is a bit ill-formed. There are more precise statements that we might take you as asking, for instance you might be claiming that the low takes place after sunrise, and be asking why that is. A very basic model of the temperature is that it is a sinusoidal function of time, and it is driven by the intensity of solar energy, also modelled as a sinusoidal function of time (that is, the net power, when the heat radiating from the Earth is subtracted from the heat coming from the Sun, is modelled as a sin function). If we had that the solar power is $P(t) = -\cos(t)$ where midnight is considered to be both $0$ and $2\pi$, and temperature is $T(t)$ where $T'(t) = P(t)$, then we would actually have $T$ and $P$ being $\pi/2$ (that is, six hours) out of phase with each other. That is, solving for $T(t)$ gives us $\sin$, and $\sin(t)$ is the same as $P(t-\pi/2)$.
The actual equation will be much more complicated: solar power isn't a sine wave, there are heat reservoir effects, radiative cooling depends on the current temperature, etc. The actual displacement between the minima will depend on all of those factors, but the general principle that the forcing function and the response function tend to be out of phase holds.
