-3

Consider this scenario: If the surface density of Earth were constant, it would follow that it would be impossible to have all land mass that is above the floor of the ocean concentrated on one side of the Earth. The water would simply flow until it centered over the mass of the earth. With this scenario the amount of land mass above the average ocean floor would need to be balanced around the sphere of the Earth, so with all of the currently above water continents on one side of the earth (Pangaea), other continent(s) would be exposed on the opposite side of the earth.

So is that scenario really the case, or is there actually enough density variation in Earth's crust to have higher density rock concentrated on the ocean side of Earth, which would allow all of the landmass above water to be concentrated on the less dense side?

  • 1
    "Assuming that the surface density is relatively constant..." is your basic problem. Continental rock is lighter than ocean crust, which is why (simplistically) it floats. Think (if you are an American) of boiling yesterday's Thanksgiving turkey carcass for stock: the lighter fatty bits float to the surface, and eventually collect in "continents", whether one or many doesn't matter. – jamesqf Nov 24 '18 at 04:37
  • 3
    Even if density were constant I for one don't see why the water would flow to be centered over the "extra" mass. The Earth is almost 4000 miles in radius. The ocean has an average depth of 2 miles. As such, relatively minuscule amounts of land are above the ocean... and the much greater gravity within the Earth will still pull water to the lowest point. Having one continent wouldn't be a giant mass imbalance pulling water towards it, but just a tiny gravitational pull. There's still a large "imbalance" even now – JeopardyTempest Nov 24 '18 at 09:32
  • 2
    Put it this way: instead of the center of mass being ideally right at the center of the Earth, the 2 miles extra of land would shift the center of mass a very small distance "continentward" from the center. But the center of mass is still deep within the Earth. Likewise I could envision perhaps there'd be a very very tiny bulge in the water upwards towards the continent. But would think the bulge would be on the order of inches or feet? The water mass can still be centered over the center of Earth mass without covering up the supercontinent. – JeopardyTempest Nov 24 '18 at 09:53
  • Jeopardy- Being very familiar with physics and engineering, I am extremely confident that given constant density, Earth's water would definitely flow to balance over the entire sphere. Nature doesn't care if an imbalance is "minuscule", it will act to balance it. The great lakes are only about 0.003% of the Earth's radius above sea level, but the Niagara falls prove that this small imbalance is being corrected. And this action would be much faster in the ocean where all that solid land wasn't in the way. –  Nov 24 '18 at 16:34
  • Jeopardy- Density of Earth is 5.51, but crust is about 2.7, about 2:1. So if the avg. land sticks out 2000', the avg. water will shift 1000'. But since ocean water only has a density of 1.0, it is even less significant to the center of mass. So it is actually more relevant to consider the amount of landmass above the average ocean floor, not sea level. So it would have been more accurate for me to say that the amount of land mass above the average ocean floor must be balanced around the sphere of the Earth. Surely someone has modeled this, haven't they? –  Nov 24 '18 at 17:13
  • jamesqf- You imply that I have neglected density when it is a major component of my question. Regarding your illustration, fat collects into groups due to surface tension. Do geologists regard surface tension as significant to the formation of continents? This seems unlikely on the geological scale. –  Nov 24 '18 at 17:47
  • 2
    @Matt Bradfield: Replace surface tension with plate tectonics :-) And consider that the mantle has convection currents, just as your stock pot does, albeit working on a much longer time scale. So the floating bits move around on the surface, clumping together or breaking apart without affecting the underlying liquid. – jamesqf Nov 24 '18 at 18:23
  • I'm not too familiar with using Wikis. So I see that apparently I can edit the various answers, which I'm not sure what to do with. David's post has a good start on answering my intended question. Should I add the detail that mantle has a density of 3.3 and add the math demonstrating how all those details explains that Oceanic areas are actually more dense than continental areas? Then we would have one post that fully answers my intended question. –  Nov 25 '18 at 14:56
  • 1
    Having read the instructions for editing another post, I'm thinking the details I would add are not minor. So I think the answer is no, I shouldn't edit that post. Let me know if you disagree. –  Nov 25 '18 at 15:03
  • I accepted the only answer which includes a demonstration (including math) of how the facts relate to the problem. My high school science teacher would never have accepted an answer without such a demonstration, nor should any lover of science. To date, it is the only such demonstration on this topic that I am aware of, but if anyone finds one published elsewhere I will gladly credit it and add a link. If anyone has suggestions on how to make this demonstration understandable to more people, I will gladly make improvements. –  Nov 26 '18 at 13:29
  • 1
    I don't understand the flow part at all. Take a volcanic mountain somewhere in the ocean. Are you suggesting that water should locally flow up the mountain so that there's a bulge in the ocean that covers the mountain? If not, I don't see anything preventing the mountain from rising above sea level. – Nuclear Hoagie Nov 27 '18 at 13:57
  • @Nuclear Wang. No. The physics and math is quite clear. If you take a sphere and ADD something to one side, the center of gravity MUST shift. It will no longer be in the center of the previous sphere. Water covering said sphere would shift toward the side where mass was added. If it shifted enough, it would even expose part of the sphere on the side away from the added mass. As an interesting side note, the sphere must have a density greater than water, otherwise all the water would collect on one side of the sphere. –  Nov 28 '18 at 00:34
  • except there sphere is not solid, its is liquid, or sufficiently liquid like that when you add something it displaces something else, the center of gravity never moves. the continents do not sit up as much they are sunken within the underlying rock like an iceberg. – John Nov 29 '18 at 00:07
  • If there was no difference in density there would be no land masses, continents are caused by a difference in density, if you try to pile the surface rock up it just sinks, you can't use it to change the earths center of gravity. – John Nov 29 '18 at 23:43
  • The earth's mantle is definitely solid. The viscosity of the mantle ranges between 10^21 and 10^24 Pa·s, depending on depth. So it behaves a little like a liquid, but it is a gross oversimplification to say that anything added will "just sink". Maybe on a scale of 100 Ma. In the mean time what else has been pushing it around? And of course you can shift the center of mass. But you don't say in relation to what. In this case we are talking about shifting the center of mass in relation to the two major surfaces, ocean and land. It definitely can and does shift. –  Nov 30 '18 at 00:07
  • Kudos to Semidiurnal Simon for actually working the science and math of this with his second answer. He has proven that the reason for asking the question is valid. Unfortunately, that answer has no votes despite being useful, and his first answer has 2, despite the fact that he himself proved it wrong. Using that hemispherical shell method, I was able to come up with an answer to my own question that is reasonably realistic, provable and satisfactory. I’m not going to waste my time posting it here unless someone asks for it though. –  Dec 02 '18 at 18:09
  • I believe this wiki proves why professors say to don’t trust wikis. It seems most posters are more concerned about proving they’re right than actually getting the science right. I won’t be wasting my time asking a complex question here again (the only kind worth asking). It could help if the wiki allows separate votes for “Useful” and “Answered the question”. While none of the contributions actually answered the question, I did find 2 of them useful. I had hoped to find people more interested in science. –  Dec 02 '18 at 18:10
  • My final analysis of the performance of the wiki: The simple rote answer that had facts easily obtainable elsewhere got the most votes, despite not answering the question by showing and quantifying how the facts relate to the question. The answer with unfounded speculation got some votes, despite being proven false by the author’s own later post. An answer which used actual math to effectively address question’s premise got 0 votes. And the answer that attempted to actually answer the question was voted down, despite no provable evidence being provided that it should be. –  Dec 02 '18 at 18:12
  • I guess I better understand why politicians can get away with denying science. Go ahead and delete this question, I would rather see that than bad science be left standing. –  Dec 02 '18 at 18:13

3 Answers3

7

Assuming that the surface density is relatively constant, it would be impossible to have all of the above water land mass concentrated on one side of the Earth.

That's a bad assumption. Four key differences between oceanic and continental crust are

  1. Chemical composition. The rock that forms oceanic crust has more calcium and magnesium but less aluminum and silica that does the rock that forms continental crust.
  2. Density. The different chemical compositions makes oceanic crust about 10% more dense than continental crust.
  3. Age. The oldest oceanic crust is 100 million years old while the oldest continental crust is over 4 billion years old. The processes that recycle ocean crust (primarily subduction) are much more efficient than are the processes that recycle continental crust.
  4. Thickness. The quick recycling of oceanic crust keeps it from building up. Most oceanic crust is between 7 to 10 kilometers thick. The slow recycling of continental crust has enabled it to build up over time. Most continental crust is between 25 to 70 kilometers thick.

The combination of different densities and different thicknesses means that the continents are elevated above the ocean floors by almost 5 kilometers on average.

David Hammen
  • 23,597
  • 1
  • 60
  • 102
  • Keep in mind, constant density is not my assumption of reality. It is a useful assumption to understand the problem. I assume there is variation in density. The relevant element of the question is "is there actually enough density variation". You have partially answered that by explaining some of the variation that does exist. It is not proven that it is "enough" though. It does give me something to think about. I will do some math and see if it is enough to prove that all the continents could be on one side of Earth. –  Nov 24 '18 at 17:35
  • @Matt Bradfield: But constant density is not a useful assumption. It is a false one, which is leading you astray. Now if the Earth was liquid, it would (absent external influences) form a perfect sphere. But it isn't, and it doesn't. All sorts of forces - rotation, tides, different densities, the forces of plate tectonics - cause it to deviate from sphericity. So instead there's a gravitational equipotential surface, and that's where the water goes. – jamesqf Nov 24 '18 at 18:29
  • Assuming constant density is a very useful assumption. If one cannot understand how a simplified (constant density) model would behave, one cannot possibly understand how a more complex (varying density) model would behave. Far from leading us astray, considering the assumption leads us to the answer, because it shows us that for all the continents to be on one side, their MUST be variation in the density. And when the variations in density and their thicknesses are calculated, it leads us directly to an answer to the problem (see my answer to the initial question). –  Nov 25 '18 at 00:13
  • 1
    @MattBradfield - Re Assuming constant density is a very useful assumption. No, it is not. The Cavendish experiment, performed over 200 years ago, demonstrably showed that the Earth's density is anything but uniform. Sometimes spherical cow assumptions are rather useful. Other times, not so much. This is one of those other times. – David Hammen Nov 25 '18 at 03:51
  • I am being misunderstood.Perhaps the preface to my question needs rewording. When I speak of assuming constant density, it is a thought exercise. It's a preface leading to the actual question. This is a common technique in scientific inquiry, leading one to the next important factor. In this case it leads to density as the next important factor to consider. The question was not "if" density varies, but "how much" and "is that enough". My calculations show it is enough. But I fear my question is unclear to others. Perhaps someone can suggest improvements that would make my intention more clear. –  Nov 25 '18 at 09:37
2

OK. Let's assume, for the sake of argument, that oceanic and continental crust does have the same density (it doesn't, but that doesn't matter). Let's further assume that everything under the earth's crust has constant density (it doesn't, but that also doesn't matter)

To a first approximation, the oceans will form a surface of constant distance from the centre of mass of the earth. Under the assumptions above, if the continents were evenly distributed then the centre of mass would be in the middle of the planet, and we would have a global ocean (minus those continents) of constant depth.

If all the continents were on one side, then there would be a miniscule change to the centre of mass of the earth, which would cause the sea level to be slightly higher on the side with the continents than the side without. I'm not going to try to calculate the magnitude of that offset, but bear in mind that the earth is a solid ball of diameter ~12,600km, while the crust is a little 35km layer on top[1]. And the crust is less dense than what's underneath. The continents will make very little difference to the position of the centre of mass.

That's a first approximation. There will also be some direct gravitational attraction between water and continent. This has been calculated (as, interestingly, has that between water and ice sheets), and it does have a measurable effect, increasing sea level close to the land by a small amount. I don't remember whether that amount is of the order of centimetres or metres (can anybody fill me in?), but either way it is not remotely close to being enough to submerge the continents.

[1] Credit to JeopardyTempest for phrasing this nicely in comments.

Semidiurnal Simon
  • 5,810
  • 1
  • 21
  • 43
  • Your proposition is completely unsupported by physics. Show me the math. Gravity simply doesn't just ignore ANY mass. –  Nov 28 '18 at 00:22
  • 4
    @matt Bradfield maths doesn't magically make physics. The problem here is not one of maths, but of a conceptual misunderstanding. I'm struggling to work out what that is, though. I think we agree that adding extra mass to one side of a sphere will shift the centre of mass of the sphere. In this case we're adding a tiny bit of mass to one side of a really massive sphere, so the CoM will shift by a very small distance. That will mean that slightly more of the surface water will rest on the side with the added mass - it will not cause all the water to rush to that side. Does that make sense? – Semidiurnal Simon Nov 28 '18 at 05:41
  • This question absolutely requires math to quantify it. I don't recall any physics problems without math and formula(s). Perhaps someone can draw this in CAD and measure the shift using more accurate 3D math.Here's a rough estimate: Let's assume earth is density 5.5 and continental crust has density 2.7, height above sea floor of 4500 m, and covers 40% of earth. 45002.7/5.540%=890 m. That's including the density factor which I ignore in the introduction to my question. The average continent is only 840 m high. The water would cover MOST of dry land. Minuscule? Hardly. –  Nov 28 '18 at 13:40
  • @MattBradfield You're completely neglecting the mass of the mantle and core, which forms the vast majority of the mass of the Earth. – bon Dec 01 '18 at 14:08
  • The density of 5.5 includes the core, so its not ignored. Your statement that the core has the majority of the mass of the Earth is false, as it has about 33%. If you really believe that the core being denser than the mantle matters, then prove it mathematically and answer the question. I don't believe the density variation between layers matters, I think that was solved mathematically hundreds of years ago, but since it would help answer the question I asked, I would welcome a mathematical proof one way or another. I do believe the density variation of opposite sides of Earth matters greatly. –  Dec 01 '18 at 17:59
0

OK, I'm sufficiently fed up with this to attempt a mathematical answer. It'll be very approximate, but it'll demonstrate an upper limit to how much the sea is skewed to one side of the planet (it's actually more than I expected). I fully expect to get something wrong here; if it's something that matters, please tell me about it!

Let's imagine a cartoon planet that consists of two parts:

  • A sphere of radius 6370 km
  • A half-shell of "continentals" with a thickness of 4 km (representing the distance from seafloor to continent)

For simplicity we'll assume that all of these have equal density, and in arbitrary units we'll define that density to be 1.

We want to find where the centre of mass of this "planet" is. Let's define our coordinate system to work in one dimension, along a line running from the middle of one half-shell to the middle of the other, where x=0 is at the centre of the sphere.

Here's a diagram (not to scale):

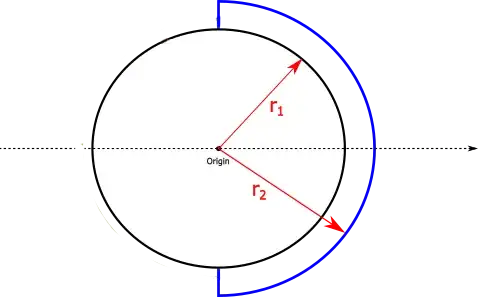
enter image description here

$r_1=6370$ km; $r_2=6374$ km

The mass of the sphere, in arbitrary mass units, is $\frac{4}{3} \pi r_1^3 = 1.1\times 10^{12}$.

The mass of the continental half-shell is $\frac{1}{2}\cdot\frac{4}{3} \pi (r_2^3 - r_1^3)=10^9$.

The centre of mass (CoM) of the sphere is at $x=0$.

I had to look up online how to find the centre of mass of a hemispherical shell, but it turns out that it lies at $x=\frac{3}{8}\frac{r_2^4 - r_1^4}{r_2^3 - r_1^3} = 3186$ km.

To find the location of the centre of mass of the combined object, we use $x_c = \frac{m_1d_1 + m_2d_2}{m_1 + m_2}$ where each $m$ is a mass and each $d$ is the position of the centre of mass of that object. So,

$x_c = \frac{1.1 \times 10^{12} \times 0 + 10^9 \times 3186}{1.1\times 10^{12} + 10^9} = 2.9 $ km.

So the centre of mass of our cartoon planet is 2.9 km closer to the "continent" side than the "ocean" side. That means that the ocean will, rather approximately, try to form a shell centred on that point, thus being 2.9 km deeper in the centre of the continent than in the centre of the ocean. Errr... Except that the sea wouldn't actually do this because it would be blocked by the giant continent that's in its way. To figure out what would actually happen would require doing the maths in 3D, and possibly involving tractive forces and the like, and that's well beyond my capability this afternoon ;-)

I emphasise once again that this is an extremely generous scenario - half of the planet is continent, which is more than on Earth, and everything has the same density, rather than the inside of the planet being denser than the crust (which would make the effect much weaker). Plus, once we're dealing with values of a few km, in the real world there are probably other variations (e.g. equatorial bulge, non-ellipsoisal geoid due to density variations, etc) that have much bigger effects.

Semidiurnal Simon
  • 5,810
  • 1
  • 21
  • 43
  • Check your assumptions. You have the ocean floor 29,000 m below the average continental surface. The oceans average about 3690 m deep, and the average land rises above the ocean by about 840 m, for a total of about 4530 m. If we do a quick compensation of your result to extrapolate, 4530 m / 29000 m * 11.4 km = 1.78 km. This seems more realistic and is more in line with what my rough calculation showed, but that calculation did account for the variation in density between the core and crust. If we compensate your result to include that 5.5/2.7*1.78=0.870 km, so pretty darn close to 890 m. –  Nov 28 '18 at 23:59
  • @MattBradfield oh, quite right about the first part - thank you. I don't agree that one can scale the result as you have, so I've revised my cartoon version to a simpler one: now we have just one half-shell, representing continents, which is just 4km thick. I've kept uniform density, because the reality is so much more complex than "the mantle has density n" - but this should still be a generous assumption - because the crust is less dense than everything beneath, the actual effect will be less. – Semidiurnal Simon Nov 29 '18 at 07:29
  • My first impression of the revision is that there must be an error in this math, because you can't add 4 km on the surface and shift the center of mass MORE than the added material (5.9 km). My experience with extrapolation comes from 30 years of engineering. You learn when you can take shortcuts to quickly estimate the difference between two scenarios. Then you can do more exact calculations once the choices are narrowed. Plus we didn't all have computers when I was young, so you had to do math by hand gasp. Assumptions are good, although I would use 6374.5 to not round difference. –  Nov 29 '18 at 13:52
  • @MattBradfield remember we're adding a half-shell of 4km thickness, not just 4km at the end of a column. I think it can shift the CoM by more than 4km.

    In any case, I can't find an error. If you can spot it, feel free to point it out :)

     – Semidiurnal Simon Nov 29 '18 at 17:32
  • You calculated the mass of a continental full sphere shell. It needs to be cut in half to be continental half-shell. A smaller factor to consider is that when calculating small differences in large systems it is important to not round your inputs or intermediate answers. The small differences can get washed out by the rounding. –  Nov 30 '18 at 03:45
  • @MattBradfield good point, thank you! Fixed, so the answer is half of what it was. As to the rest of your comment... hah. Using a continent thickness of 4 rather than 4.5 is hardly the biggest approximation here! – Semidiurnal Simon Nov 30 '18 at 06:56
  • It's a minor point, but even with your assumptions (4 instead of 4.5), using unrounded intermediary results gives an answer of 3.00, not 2.9. That was using a spreadsheet with about 16 digit precision. I just don't believe in rounding things that you know well. As you state, there are plenty of things we don't know well, but we might as well state what we do know as accurately as possible. Not that it changes the result much, and this result is quite a bit more than I expected. Using your assumptions here and my previous estimating method, I would have estimated 4000 m x 50%= 2000 m. –  Nov 30 '18 at 12:28
  • So this confirms my reason for asking the question. And the math provides a good answer. But it's the answer to a different question, which is "If the continents were all on one side of the earth, and the density of the earth were constant, how much would the water shift?" The answer to my full question is still unanswered, and it is obviously a complicated answer. Based on your stated distance of 2.9 km, the continents would all be covered up. The oceans are 3.7 km deep. 2.9 + 3.7 = 6.6 km. 6.6 km > 4 km. Hmmm, wasn't there a major extinction near that time ...? –  Nov 30 '18 at 12:40