1

https://www.quora.com/How-is-signal-filtering-done-with-convolution

What is the relation between convolution and a filter? Is it mainly that convolution process is used to determine the output of an LTI system and since filters are also LTI systems?

A related statement mentioned in above link and also shown in attached snap

enter image description here

DSP_CS
  • 1,910
  • 2
  • 29
  • 65
  • The output of a filter can be calculated by convolving the input with the filter's impulse response. Convolution is one way to implement a filter. Does that answer your question ? – Hilmar Mar 11 '23 at 16:45
  • If Convolution is one way to implement a filter, what are the other ways? – DSP_CS Mar 11 '23 at 16:50
  • In signal processing, convolution is often used to filter out noise or unwanted frequencies from a signal? – DSP_CS Mar 11 '23 at 16:53
  • Other methods: Convolution only works only for FIR filters, IIR filters have different algorithms ( biquads in different Form, lattice, etc.). Warped FIRs are hybrids. Long FIR can be more efficiently done with overlap-add or overlap-save. – Hilmar Mar 11 '23 at 18:53
  • 2
    I'm a bit confused. You asked about convolution before, and it was clear you understood how LTI systems and convolution relate. – Marcus Müller Mar 11 '23 at 19:54

2 Answers2

2

Convolution does predict the output of a linear time invariant system based on the input convolved with the impulse response of the system, and such systems are commonly referred to as "filters":

$$y[n] = x[n]*h[n]$$

Where $y[n]$ represents the output, $x[n]$ the input, $h[n]$ the unit sample response (discrete impulse response) and "*" represents convolution.

The graphic below provides an intuitive understanding on convolution and its use with filters. The impulse response for a system is what would appear at the output of a system given an impulse is applied at the input. Consider an arbitrary input waveform as a weighted series of impulses delayed in time, such that the output at any given time is due to the current input summed together (via superposition) with the trailing response of prior inputs. This operation is captured mathematically in convolution.

Convolution

Both IIR and FIR filters are represented with convolution operations as I show in the graphic below:

FIR vs IIR

The key difference is the convolution for the case of an IIR extends to infinity due to the infinite impulse response (IIR) so it can't be realized directly from the convolution equation as shown, while the FIR in comparison is done over a finite number of samples, so is directly realizable from the generalized convolution summation.

It is impossible to realize an IIR filter directly from the convolution summation, but a subclass of IIR systems can be implemented using recursive difference equations as:

$$y[n]= x[n] - \sum_{k=1}^Na[k]y[n-k]$$

By feeding back the output of previous outputs, the result is the same as would be achieved with the convolution of an infinitely long impulse response (and the filter itself can generate an infinitely long impulse response with a finite number of coefficients).

The generalized expression that includes both feed-forward (FIR) and feed-back (IIR) components is the Generalized difference equation given as:

$$y[n] = \sum_{k=0}^{M-1}b_k x[n-k] - \sum_{k=1}^N a_k y[n-k]$$

Of practical interest, taking the z- transform of the Generalized Difference Equation as given above leads to the transfer function in the format commonly used in MATLAB, Octave and Python scipy.signal for IIR and FIR filters (where $b$ is the coefficients of the feed-forward FIR filter and $a$ is the feed-back coefficients of the IIR filter:

$$\frac{Y(z)}{X(z)} = H(z) = \frac{\sum_{k=0}^{M-1}b_k z^{-k}}{1+\sum_{k=1}^N a_k z^{-k}}$$

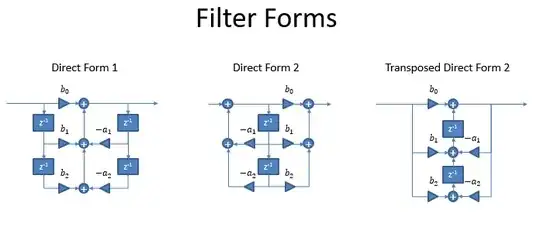
This then leads directly to the common "Direct-Form" implementations as shown in the graphic below. As MattL notes in the comments, there are additional realizations that unlike these do not derive directly from the convolution equation or generalized difference equation (for example: parallel form, frequency sampling structure, lattice and lattice-ladder, polyphase, etc) but all are ultimately mathematically equivalent to a convolution in operation.

Direct Form realizations

Dan Boschen
  • 50,942
  • 2
  • 57
  • 135
  • Good answer +1, but maybe you should generalize the difference equation for IIR filters by adding a sum of delayed input signals on the right-hand side. – Matt L. Mar 11 '23 at 20:49
  • It's good that you pointed out that the input-output relation of ALL LTI systems is correctly described by convolution. But that doesn't mean that we always can or want to implement a filter by directly computing the convolution sum. – Matt L. Mar 11 '23 at 20:52
  • @MattL. Thanks Matt! Yes agree- I always viewed that as the FIR component, but noted that even if a filter includes FIR components is still an IIR. I'll add that to show that complete implementation. – Dan Boschen Mar 11 '23 at 21:09
0

Discrete convolution is equivalent with a discrete FIR filter. It is just a (weighted) sliding sum.

IIR filters contains feedback and can not be implemented using convolution.

There can be many others kinds of signal processing systems that it makes sense to call «filter». Som of them time variant (possibly adaptive), or non-linear.

Knut Inge
  • 3,384
  • 1
  • 8
  • 13
  • Some terminology nerdiness: first, a system can be linear and time-varying, and in fact a linear time-varying system can be described by convolution -- it's just that the impulse response depends on both the delay and the absolute time of the impulse; second, your response reads like a system can be time varying and adaptive, or it can be nonlinear -- but adaptive filters are nonlinear; finally, a filter can be one of the four possible combinations of linear vs. non-linear or time varying vs. time invariant. LTI systems are easiest to analyze, time-varying non-linear systems are hardest. – TimWescott Mar 12 '23 at 04:49