0

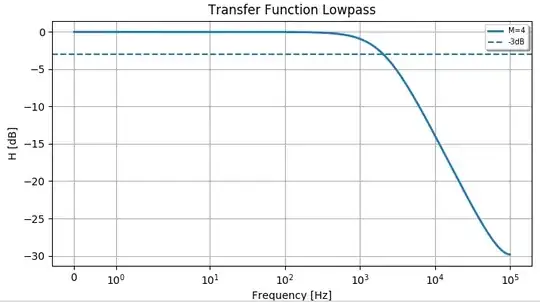
The transfer function $$H_{LPF}=\frac{b_0}{1+a_1z^{-1}}$$ becomes a multiplier-less low-pass filter if $b_0=2^{-M}$ and $a_1=2^{-M}-1$. According to this paper, the cut-off frequency is then given by $f_c=\frac{f_s}{2^M - 1}$. I tried to verify that in a python script, but I get different results. In my case, the cut-off frequency for $f_s=200kHz$ and $M=4$ is roughly at $2kHz$, whereas according to the formula it should be $13.3kHz$. Why do I get a different result?

enter image description here

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.fftpack import fft

def lpf(in_signal):
    M = 4
    b = [2**(-M)]
    a = [1, 2**(-M) - 1]


return signal.lfilter(b, a, in_signal)




fs = 200e3
N_tf = 4096
u = np.concatenate(([1], np.zeros(N_tf - 1)), axis=None)


freq = np.fft.fftfreq(N_tf, 1/fs)
freq_axis = freq[0:N_tf//2]


plt.figure(figsize=(14,6), num = 'Transfer Function Lowpass')


y = lpf(u)
tf = 20*np.log10(abs(fft(y))[0:N_tf//2])
plt.plot(freq_axis, tf, linewidth = 2, label = 'M=4')
plt.axhline(-3, linestyle = 'dashed', label = '-3dB')
plt.xscale("symlog")
plt.legend(loc='upper right', shadow=True, fontsize='x-small')
plt.grid(which='both',axis='both')
plt.xlabel('Frequency [Hz]')
plt.ylabel('H [dB]')
plt.title('Transfer Function Lowpass')


plt.show()
MisterFilter
  • 413
  • 3
  • 16

2 Answers2

1

As you've seen in the linked answer the -3 dB point is given by the formula:

$$f_{-3\;\text{dB}}=\arccos\left(1-\dfrac{\alpha^2}{2-2\alpha}\right)=\arccos\left(1-\dfrac{2^{-8}}{2-2^{-3}}\right)=0.064561\cdot\dfrac{f_s}{\pi}=2055\;\text{Hz}$$

The formula given in the paper is wrong but, in fairness, I've seen it approximated in various ways, involving $2\pi$ or not. However, if you replace $f_s$ with $f_s/(2\pi)$ you do get close to the real number:

$$\dfrac{f_s}{2\pi}\cdot\dfrac{1}{2^{-M}-1}=\dfrac{2\cdot 10^5}{2\pi}\cdot\dfrac{1}{2^{-4}-1}=2122\;\text{Hz}$$

I haven't tested it further but, given the characteristic of the $\arccos(x)$ (with the above argument), the closer $x$ is to $1$, the closer the answer is to a slope at origin ($x$, itself). So, if the coefficient is $2^{-4}=0.0625$ then the value is $1-0.0625^2/(...)\approx 1$, and $\arccos(1)=0$.

a concerned citizen
  • 1,828
  • 1
  • 9
  • 15
  • I can't find the proper words but, about this part: "given the characteristic of the $\arccos(x)$" -- I mean that if you plot the real formula from $[0...1]$ you'll see a curve similar to an $\arcsin(x)$, which diverges from the unity slope ($x$) the farther it is from the origin. – a concerned citizen Aug 09 '22 at 16:46
0

I didn't read the whole paper, but for a low-pass filter of the form $H(z) = \frac{b z}{z - a}$, the cutoff frequency is more like $f_0 = \frac{1 - a}{2 \pi} f_s $.

So between you and the author, a factor of $2 \pi$ got dropped.

TimWescott
  • 12,704
  • 1
  • 11
  • 25