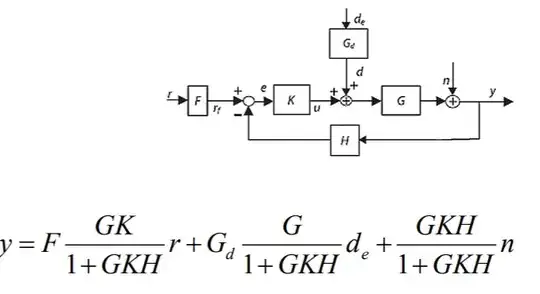
For the following system, I am not quite sure how the equation representing the input output relation is derived. Here, r is an input reference signal, $d_e$ is external disturbance and $n$ is noise. What I can write is $G[K(-Hy + Fr)+G_dd_e]+n = y$ so $(1+GKH)y = GKFr + GG_dd_e +n$ so $y = F\frac{GK}{(1+GKH)}r + G_d\frac{G}{(1+GKH)} + \frac{1}{(1+GKH)}n$ however, the correct answer for the $\frac{1}{(1+GKH)}n$ term seems to be $\frac{GKH}{(1+GKH)}n$? What have I done wrong?
