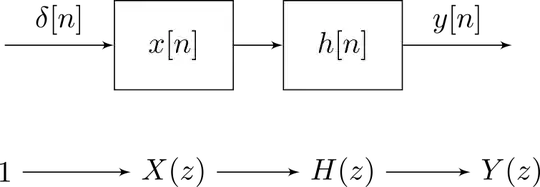Why is convolution commutative, as it seems to treat two signals in a different way in an LTI system?
If you imagine $y[n] = x[n] \star h[n]$ with $x[n]$ being an input signal and $h[n]$ being the impulse response of an LTI system A, how does it make sense that LTI system B with input $h[n]$ and impulse response $x[n]$ generates the exact same output $y[n]$ ?
In a discrete-time system such as the one that you have, the number $y[n_0]$ (here $n_0$ is a fixed integer) is a sum of the form $$\sum_{k=-\infty}^\infty h[k]x[n_0-k]$$ which can be re-arranged via a change of variables (replace $k$ by $n_0-\ell$) to $$\sum_{\ell=-\infty}^\infty h[n_0-\ell]x[\ell].$$ So, the commutativity of the convolution is trivial. The issue is the interpretation that you put on it. As Laurent Duval/s answer points out, the systems A and B are not equivalent in any sense of the term. If the signal $x$ were replaced by a different signal $\hat{x}$, then system A would have output $\hat{y} = h \star \hat{x}$, but you wouldn't get the same output $\hat{y}$ if system B were excited by $h$; the impulse response of system B continues to be $x$, and system B thus has output $x \star \hat{x} = \hat{x}\star x \neq h \star \hat{x}$.
Imagine a system that accepts a single number $x$ as its input, and it multiplies that number with another number $h$. Would it surprise you that another system which multiplies its input with the number $x$ gives the same output as the first system when fed with the number $h$ as input? If not, then it also shouldn't come as a surprise that the output of an LTI system with impulse response $h[n]$ and input $x[n]$ gives the same output as another LTI system with impulse response $x[n]$ and input $h[n]$.
Or, in mathematical language, for the discrete-time case:
$$(x\star h)[n]=\sum_kx[k]h[n-k]\;{\Big|}_{m=n-k}=\sum_mx[n-m]h[m]=(h\star x)[n]$$
There are fundamental differences in concept between signals and systems. I will explain this through the idea of unit consistency (see for instance). However, for LTI systems, signals and systems become dual through convolution, since the latter is commutative. Two digressions first, due to the mention in @Dilip Sarwate answer.
If two different systems provide the same outputs for some input signals, this means they share some properties. But if their outputs are equal for all inputs, then they essentially have the same impulse response, and they are virtually the same systems.
For instance, imagine you have an input sine at frequency $f$. If both systems cut frequency above $f-\epsilon$, both have the same behavior for that signal, but they can be two different low-pass systems, more signals are needed to distinguish them.
For instance, a constant signal equal to one, or a 2-periodic signal with {$2,0$} values produce the same output for $2n$-averaging filers.
Back to your question. A system $\mathcal{S}$ turns inputs $X$ into outputs $Y$, respectively with physical units $u_X$ and $u_Y$. So a system can be seen as a unit converter, formally with inner unit $u_Y/u_X$. Generally, the system is "fixed", while inputs my vary. So, there is no reason why $\mathcal{S}$ and $X$ should play the same role.
However, when one considers LTI systems, suddenly system properties can be somehow transfered to signals, and vice-versa (as long as the convolution is well-defined). This is related to the fact that convolution commutes with shifts. For simplicity, imagine a "three-tap" system, with $z$-transform response $h_{l}z^{-l}+h_{m}z^{-m}+h_{n}z^{-n}$. You can directly convert this into a three-band filter bank, with a single input and respective answers $h_{l}z^{-l}$, $h_{m}z^{-m}$ and $h_{n}z^{-n}$. Each branch only provides, for each input, a scale factor and a delay.
But the same happens to signals: each input $x=\{\ldots,x_{l},\ldots,x_{m},\ldots,x_{n},\ldots\}$ can be split into scalar components:
$$x=\ldots+x_{l}\delta_{l}+\ldots+x_{m}\delta_{m}+x_{n}\delta_{n}+\ldots$$ where $\delta_{\cdot}$ denotes the Kronecker symbol. Due to linearity, each component could be fed through the linear system. When everything (signal and system) is split this way, computations are just a bunch of $x_{k}\delta_{k}$ going through a couple of $h_{i}z^{-i}$, which fundamentally are the same operations: a factor/an amplitude and a delayed sample/a delay operator. In other words, $x_{k}\delta_{k}$ going through $h_{i}z^{-i}$ yields the same result as $h_{k}\delta_{k}$ going through $x_{i}z^{-i}$, because the product $h_{k}x_{i}$ is commutative (and preserves unit consistency), and delays commute as well.
In other words, an LTI just yields a weighted sum with weights $h$ on input samples of $x$: $\sum h_i x_{k-i}$, which can be read as well as a weighed sum with weights $x$ on input samples of $h$: $\sum x_i h_{k-i}$. For unit consistency though, one should switch the units of $x$ and $h$.
This interchangeability between signals and systems in the LTI seems to be at play (at first glance) in the polyphase/modulation expression of filter banks, or in matched filtering.
Think of the convolution $x\star h$ as taking some delayed copies of $x$ summed together, each with an amplitude read out from the entry of $h$ at that delay. Let's picture it with sparse-impulse signals:
(Ignore the vertical shift, that's just to de-clutter the plot)
Now, if you turn around the convolution, all that changes is the notion of which time-scale is “delay of the signal” and which simply “time of the original signal”. You end up with the same result.
Source code (Haskell with dynamic-plot):
import Graphics.Dynamic.Plot.R2
import Control.Monad
import Data.List
import System.Random
main :: IO ()
main = do
-- Times of the impulses in signal
txs <- scanl (+) 0 <$> replicateM 16 (randomRIO (0,0.1))
-- Amplitudes of the impulses in
xs <- replicateM 8 (randomRIO (0,1))
-- Times of the echoes in convolution kernel ℎ
ths <- scanl (+) 0 <$> replicateM 16 (randomRIO (0,0.4))
-- Amplitudes of the echoes in ℎ
hs <- (1:) <$> replicateM 9 (randomRIO (0,1.0))
plotWindow [plotLatest
[ plotDelay 0.5 $ plotMultiple
[ legendName name $ lineSegPlot
[(t,y+y0) | (t,x) <- sig, y<-[0,x,0]]
| ( sig, name, y0 ) <-
[ ( zip txs xs, "" , 0 )
, ( zip ths hs', "ℎ" , 1 )
, ( [ (tx+th,x*h)
| (tx,x)<-zip txs xs
, (th,h)<-zip ths hs' ], "⋆ℎ", 0.5 )
]
]
| hs' <- cycle . tail $ inits hs]
, xInterval (0,2) ]
return ()
I very strongly recommend1 defining convolution in a slightly different way, namely as: $$(x\star h)[n]=\sum_{i+j=n}x[i]h[j]$$
You can see that this is just the standard definition with a change of variables, i.e. choose $j=n-i$. (You do need to be a bit clearer about the range $i$ and $j$ are running over, i.e. it makes a difference if $i,j\in\mathbb N$ versus $i,j\in\mathbb Z$.)
This definition makes commutativity obvious. Nevertheless, another perspective on this is that if you have a polynomial $X(z)=\sum_i x[i]z^i$ and a polynomial $H(z)=\sum_i h[i]z^i$ and you multiply them as polynomials, $X(z)H(z)$, you get $$X(z)H(z)=\sum_i (x\star h)[i]z^i$$ (This generalizes to formal power series.) Just write out the multiplication yourself in some examples to verify this and maybe prove it inductively. This perspective again makes commutativity completely obvious. This perspective also makes the convolution theorem for the Z-transform pretty obvious too.
1 I wrote a whole blog post about this.
As a complement to the previous answers, barely looking at the output doesn't allow you to identify what you had as input/system-function. Take for example the following (interconnection of) systems producing all the same output.
For the system above we have: $$ y[n] = (x \star h) [n] $$ $$ Y(z) = X(z). H(z) = H(z) . X(z) $$
For the system above we have: $$ y[n] = ((\delta \star x) \star h) [n] $$ $$ Y(z) = 1 . X(z) . H(z) = X(z). H(z) = H(z). X(z) $$
For the system above we have:
$$
y[n] = ((\delta \star \alpha x) \star \frac{1}{\alpha} h) [n]
$$
$$
Y(z) = 1. \alpha X(z) . \frac{1}{\alpha} H(z) = X(z). H(z) = H(z). X(z)
$$
A lot of other combinations giving the same result are possible of course, including interchanging the roles of $h[n]$ and $x[n]$.
Note that this observation is the main concern of the field called Blind system identification: try identifying the input and/or the system-function using only the output data.
Since we cannot solve the problem as stated, more side information (e.g., output statistics) is needed, more diverse channels also (to compensate for zeros, i.e. frequencies for which no signal can pass through), and a rich enough input signal that may be helpful for recovering the system function.
To have an intuition for your question as to
Why is convolution commutative, as it seems to treat two signals in a different way in an LTI system?
look at $Y(z)=X(z)H(z)$ as the output of two LTI systems in series. You can interchange them, applying the second then the first; that's commutativity. Also, if $X(z)$ and $H(z)$ both have the same (or an infinite) frequency-band then we can recover them (up to a scalar multiplication), otherwise, we will definitely lose some frequencies and total recovery is not possible.
You are right. It's completely absurd to think that the impulse response of an LTI system can be replaced by the input signal and vice versa and yet they produce the same result.
As an example, consider a lowpass filter with IIR impulse response $h[n]$ which is fed by the samples of speech waveform $x[n]$ to produce a lowpass filtered verison of the speech. Yet interchanging the roles of input speech and LTI system impulse resoponse $h[n]$ renders into an absurdity in a practical setting.
Yet that's mathematically the case. And you can even find example application that can take benefit of such an interchange. A mathematical explanation is given in Matt's answer.