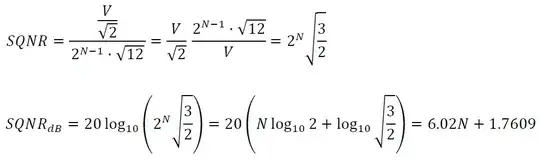I'm studying the quantization of an audio signal and in particular the SQNR (Signal to Quantization Noise Ratio).
The book on which the study says that:
where:
I don't understand how these calculations were carried out. Is SQNR not simply the "digital" version of the RMS? I know the RMS is calculated as power signal divided by power error, am I wrong?
The signal voltage is a sinusoid signal variant from $-V$ to $+V$, thus the RMS value
$$V_{rms} = \frac{V}{\sqrt{2}} = \frac{2^N \Delta V / 2}{\sqrt{2}}$$
because $2V = 2^N\Delta V$ where $\Delta V$ is quantization step.
Quantization noise is modeled as uniform random variable in $[-\Delta V /2, +\Delta V /2]$ thus its standard deviation is $V_n = \Delta V / \sqrt{12}$.
SQRN is defined as $\mathrm{SQNR}=\frac{V_{rms}^2}{V_n^2}$
$$\sqrt{\mathrm{SQNR}}=\frac{V_{rms}}{V_n} = 2^N \sqrt{\frac{3}{2}}$$
$$\mathrm{SQNR}_{dB}=20\log_{10}\left(\frac{V_{rms}}{V_n}\right) = 20\log_{10}\left(2^N \sqrt{\frac{3}{2}}\right) = 6.02N + 1.76$$
You must have mistyped your question.
