How to build a median filter function?

Question

What algorithms are there for 1-d median filtering (sliding median, rolling median, running median), similar to MATLAB's medfilt1? Of interest would be a reference implementation written from scratch, preferentially for MATLAB.

Answer 1

Here's a rolling median algorithm in C++ with $O(N)$ complexity per step, where $N$ is the length of the median filter (only odd supported). By each step you need to update() the filter with one input value and get returned a new median, which is also stored in the variable median. The algorithm keeps the median in a variable median and keeps a history of $N$ last inputs in a circular buffer. Upon new input the algorithm does the following:

1. Remove the oldest value from the history (but don't forget it just yet) and update the history with the new input.

2. If the new input is above median and the removed value is equal to or below median:

   2.1. If the number of values in the history that are above median is greater than $(N-1)/2$, set median to the lowest of those.

3. Else if the new input is below median and the removed value is equal to or above median:

   3.1. If the number of values in the history that are below median is greater than $(N-1)/2$, set median to the highest of those.

4. Return median.

The counting in the complementary steps 2.1. and 3.1. is for handling duplicates of the median in the history. If neither steps are entered, the new input and the removed value were both above or both below median, which therefore remained unchanged.

The algorithm can easily be converted to work with floats, doubles, etc. instead of ints, just remember to replace INT_MAX and INT_MIN with what's appropriate. All ints (but not unsigned ints) should be changed to the new data type.

I tested the running times of this and Ashelly's code from Robert's answer. The break-even point appears to be at $N=35$. For larger $N$, Ashelly's $O(\log N)$ code is faster, and for smaller $N$, mine is faster:

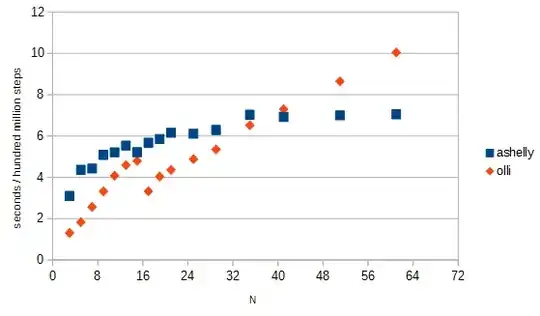
Figure 1. Run time comparison (less is better). Compilation was done by g++ -O3 and the code was run in a x64 Intel i7 PC.

My code won't give you a shorter median filter in the beginning. Instead, it will assume a history of zero input.

#include <limits.h>

const unsigned int N = 9; // odd please
const unsigned int sideN = (N-1)/2;
int history[N];
unsigned int historyIndex;
int median;

void init() {
  // Assume zeros before actual input. If you need to init with other values,
  // just feed those in using update()
  for (unsigned int i = 0; i < N; i++) {
    history[i] = 0; 
  }  
  historyIndex = 0;
  median = 0;
}

int update(int addValue) {  
  int removeValue = history[historyIndex];
  history[historyIndex] = addValue;
  if (addValue > median && removeValue <= median) {
    int lowestAboveMedian = INT_MAX;
    unsigned int numAboveMedian = 0;
    for (unsigned int i = 0; i < N; i++) {
      if (history[i] > median) {
        numAboveMedian++;
        if (history[i] < lowestAboveMedian) {
          lowestAboveMedian = history[i];
        }
      }
    }
    if (numAboveMedian > sideN) {
      median = lowestAboveMedian;
    }
  } else if (addValue < median && removeValue >= median) {
    int highestBelowMedian = INT_MIN;
    unsigned int numBelowMedian = 0;
    for (unsigned int i = 0; i < N; i++) {
      if (history[i] < median) {
        numBelowMedian++;
        if (history[i] > highestBelowMedian) {
          highestBelowMedian = history[i];
        }
      }
    }
    if (numBelowMedian > sideN) {
      median = highestBelowMedian;
    }
  }
  historyIndex++;
  if (historyIndex >= N) {
    historyIndex = 0;
  }
  return median;
}

// The rest is only for testing of the median algo

#include <stdio.h>
#include <algorithm>
#include <vector> 
#include <stdlib.h>
#include <time.h>

int main() {
  const unsigned int NData = 1000;
  printf ("N = %u, sideN = %u\n", N, sideN);
  srand (time(NULL));
  init();
  for (unsigned int i = 0; i < NData; i++) {
    int input = rand() % 10;
    printf("input = %d, median = %d, sortedHistory =", input, update(input));
    std::vector<int> sortedHistory;
    for (unsigned int j = 0; j < N; j++) {
      sortedHistory.push_back(history[j]);
    }
    std::sort(sortedHistory.begin(), sortedHistory.end());
    for (unsigned int j = 0; j < N; j++) {
      if (j == sideN) {
        printf(" (%d)", sortedHistory[j]);
      } else {
        printf(" %d", sortedHistory[j]);
      }
    }
    printf("\n");
    if (sortedHistory[sideN] != median) {
      printf("Mismatch!\n");
      return -1;
    }
  }
  printf("%u tests OK!\n", NData);
}

Answer 2

here is code for a "rolling median" copied from the reference of the reference i made above. i believe the computational cost of the alg (per sample) is $O(\log_2(N))$.

//Copyright (c) 2011 ashelly.myopenid.com under <http://w...content-available-to-author-only...e.org/licenses/mit-license>

#include <stdlib.h>

//Customize for your data Item type
typedef int Item;
#define ItemLess(a,b)  ((a)<(b))
#define ItemMean(a,b)  (((a)+(b))/2)

typedef struct Mediator_t
{
   Item* data;  //circular queue of values
   int*  pos;   //index into `heap` for each value
   int*  heap;  //max/median/min heap holding indexes into `data`.
   int   N;     //allocated size.
   int   idx;   //position in circular queue
   int   ct;    //count of items in queue
} Mediator;

/*--- Helper Functions ---*/

#define minCt(m) (((m)->ct-1)/2) //count of items in minheap
#define maxCt(m) (((m)->ct)/2)   //count of items in maxheap 

//returns 1 if heap[i] < heap[j]
int mmless(Mediator* m, int i, int j)
{
   return ItemLess(m->data[m->heap[i]],m->data[m->heap[j]]);
}

//swaps items i&j in heap, maintains indexes
int mmexchange(Mediator* m, int i, int j)
{
   int t = m->heap[i];
   m->heap[i]=m->heap[j];
   m->heap[j]=t;
   m->pos[m->heap[i]]=i;
   m->pos[m->heap[j]]=j;
   return 1;
}

//swaps items i&j if i<j;  returns true if swapped
int mmCmpExch(Mediator* m, int i, int j)
{
   return (mmless(m,i,j) && mmexchange(m,i,j));
}

//maintains minheap property for all items below i/2.
void minSortDown(Mediator* m, int i)
{
   for (; i <= minCt(m); i*=2)
   {  if (i>1 && i < minCt(m) && mmless(m, i+1, i)) { ++i; }
      if (!mmCmpExch(m,i,i/2)) { break; }
   }
}

//maintains maxheap property for all items below i/2. (negative indexes)
void maxSortDown(Mediator* m, int i)
{
   for (; i >= -maxCt(m); i*=2)
   {  if (i<-1 && i > -maxCt(m) && mmless(m, i, i-1)) { --i; }
      if (!mmCmpExch(m,i/2,i)) { break; }
   }
}

//maintains minheap property for all items above i, including median
//returns true if median changed
int minSortUp(Mediator* m, int i)
{
   while (i>0 && mmCmpExch(m,i,i/2)) i/=2;
   return (i==0);
}

//maintains maxheap property for all items above i, including median
//returns true if median changed
int maxSortUp(Mediator* m, int i)
{
   while (i<0 && mmCmpExch(m,i/2,i))  i/=2;
   return (i==0);
}

/*--- Public Interface ---*/


//creates new Mediator: to calculate `nItems` running median. 
//mallocs single block of memory, caller must free.
Mediator* MediatorNew(int nItems)
{
   int size = sizeof(Mediator)+nItems*(sizeof(Item)+sizeof(int)*2);
   Mediator* m=  malloc(size);
   m->data= (Item*)(m+1);
   m->pos = (int*) (m->data+nItems);
   m->heap = m->pos+nItems + (nItems/2); //points to middle of storage.
   m->N=nItems;
   m->ct = m->idx = 0;
   while (nItems--)  //set up initial heap fill pattern: median,max,min,max,...
   {  m->pos[nItems]= ((nItems+1)/2) * ((nItems&1)?-1:1);
      m->heap[m->pos[nItems]]=nItems;
   }
   return m;
}


//Inserts item, maintains median in O(lg nItems)
void MediatorInsert(Mediator* m, Item v)
{
   int isNew=(m->ct<m->N);
   int p = m->pos[m->idx];
   Item old = m->data[m->idx];
   m->data[m->idx]=v;
   m->idx = (m->idx+1) % m->N;
   m->ct+=isNew;
   if (p>0)         //new item is in minHeap
   {  if (!isNew && ItemLess(old,v)) { minSortDown(m,p*2);  }
      else if (minSortUp(m,p)) { maxSortDown(m,-1); }
   }
   else if (p<0)   //new item is in maxheap
   {  if (!isNew && ItemLess(v,old)) { maxSortDown(m,p*2); }
      else if (maxSortUp(m,p)) { minSortDown(m, 1); }
   }
   else            //new item is at median
   {  if (maxCt(m)) { maxSortDown(m,-1); }
      if (minCt(m)) { minSortDown(m, 1); }
   }
}

//returns median item (or average of 2 when item count is even)
Item MediatorMedian(Mediator* m)
{
   Item v= m->data[m->heap[0]];
   if ((m->ct&1)==0) { v= ItemMean(v,m->data[m->heap[-1]]); }
   return v;
}


/*--- Test Code ---*/
#include <stdio.h>
void PrintMaxHeap(Mediator* m)
{
   int i;
   if(maxCt(m))
      printf("Max: %3d",m->data[m->heap[-1]]);
   for (i=2;i<=maxCt(m);++i)
   {
      printf("|%3d ",m->data[m->heap[-i]]);
      if(++i<=maxCt(m)) printf("%3d",m->data[m->heap[-i]]);
   }
   printf("\n");
}
void PrintMinHeap(Mediator* m)
{
   int i;
   if(minCt(m))
      printf("Min: %3d",m->data[m->heap[1]]);
   for (i=2;i<=minCt(m);++i)
   {
      printf("|%3d ",m->data[m->heap[i]]);
      if(++i<=minCt(m)) printf("%3d",m->data[m->heap[i]]);
   }
   printf("\n");
}

void ShowTree(Mediator* m)
{
   PrintMaxHeap(m);
   printf("Mid: %3d\n",m->data[m->heap[0]]);
   PrintMinHeap(m);
   printf("\n");
}

int main(int argc, char* argv[])
{
   int i,v;
   Mediator* m = MediatorNew(15);

   for (i=0;i<30;i++)
   {
      v = rand()&127;
      printf("Inserting %3d \n",v);
      MediatorInsert(m,v);
      v=MediatorMedian(m);
      printf("Median = %3d.\n\n",v);
      ShowTree(m);
   }
}

Answer 3

i presume you mean an efficient sliding median? i have asked the same question at the SE.SE.

they pointed to some papers, but i don't know how to do an $O(\log_2(N))$ algorithm.

the brute force way to do a median is to sort the buffer of data (with quicksort it's $O(N \log_2(N))$ like the FFT) and pick out the value that is precisely in the middle of the sorted buffer of data. If the buffer has an even number of samples, you average the two middle values.

if your buffer isn't long (like $N$ = 5 or 15), a simple $O(N^2)$ method is to scan for the maximum $\frac{N+1}{2}$ times, each time re-marking your max value with the most negative possible value (that causes the next highest value to become the new maximum for the next scan). do that $\frac{N+1}{2}$ times and the last remaining maximum value is the median. it's easy code but not particularly efficient, so the buffer length has to be small. This is a destructive scan alg, so you have to copy the data over to a temp buffer, each sample.

Answer 4

Let us separate functions. Sorting algorithms are considered known in many places, and commonly available through efficient librairies. Since @robert bristow-johnson provided the sorting part, here is a Matlab version using Matlab sort.m, that adapts to the borders (when there is not enough samples for the full median). Interestingly, you can access to a lot of efficient Sorting algorithms, some exploiting the data type (eg integer or not) or being approximate, see for instance:

• Fast Computation of the Median by Successive Binning
• Median Filtering in Constant Time

Here is the code, with hopefully meaningful variable names and comments:

lWindow = 3; % Maximum size of the window; preferably odd for uniqueness; would be adapted at the borders
nSample = 25; % Number of data sample
data = randn(nSample,1)+(1:nSample)'; % Your data
dataRunningMedian = zeros(size(data));

if ~mod(lWindow,2)
error('Even median length is not supported right now');
else
lWindowHalf = (lWindow-1)/2;
end

% For each sample of the data
for iSample = 1:nSample
% Choose a frame around the sample, of maximum length 'lWindow'
% max(iSample-lWindowHalf,1) avoids indices below 1
% min(iSample+lWindowHalf,nSample)  avoids indices above nSample
lFrameIndex = (max(iSample-lWindowHalf,1):min(iSample+lWindowHalf,nSample));
% Get the data frame
dataFrame = data(lFrameIndex);
% Here, use any from-the-book sorting algorithm, or the one from @robert bristow-johnson
dataFrameSort = sort(dataFrame);
% Pick the central samples, and their average if they are two (even frame length)
lFrameLengthHalf = length(lFrameIndex)/2;
lFrameCentralIndex = [floor(lFrameLengthHalf),ceil(lFrameLengthHalf)];
dataRunningMedian(iSample) = mean(dataFrameSort(lFrameCentralIndex));
end

plot([data,dataRunningMedian]);axis tight; grid on
xlabel('Sample index')
ylabel('Amplitude (u.a.)')
legend('Data','Run. Med.')