How to calculate biquad coefficients for the partial (1%, 10%) applying of pre-emphasis effect

Question

I'm using sox to emulate RIAA pre-emphasis and de-emphasis effects on audio files. For pre-emphasis I call it like this:

sox --plot octave in.wav out_biquad.wav biquad 1 -1.700724 0.7029382 0.2380952 -0.1718791 -0.0442981

The biquad coefficients are taken from http://jiiteepee.tripod.com/de-pre-emphasis.html. I wonder if there is any easy way to calculate the biquad coefficients if I want to apply pre-emphasis only partially - in the range from 0% (no pre-emphasis) to 100% (full pre-emphasis).

The case for 0% seems to be easy, coefficients 1 0 0 1 0 0 would work just fine. But I'm not sure how to approach calculation of biquad coefficients for the combination of zero_filter + float_fraction * full_filter.

Answer 1

I have too few points for to comment so I try give you at least a partial answer.

You can't change those b coefficients using equal multiplier with a's. As those final coefficients comes from transformation there might be some ratios you loose in that process. In my MZT based example below, you get the final coefficients from equations

b1 = -(pole1 + pole2)
b2 = pole1 * pole2

So, you can't restore the original ratio from b1 nor from b2 --> remember also that when swap the a's and b's to get pre-emphasis filter from de-emphasis filter (or vice versa) you need to do it using those coefficients having a0 and b0 = 1.0 (i.e. not tose normalized to have 0dB at 1kHz).

So, I would suggest you to manipulate coefficients before transformation. You'll find needed coefficients for that filter mentioned in your post here from.

Here's an example based on MZT transfer (you'll find the missing info through my posts here).

pole1 = 0.99289462847423215
pole2 = 0.73908439754585875
zero1 = 0.93117565229670540
zero2 = 0.0;

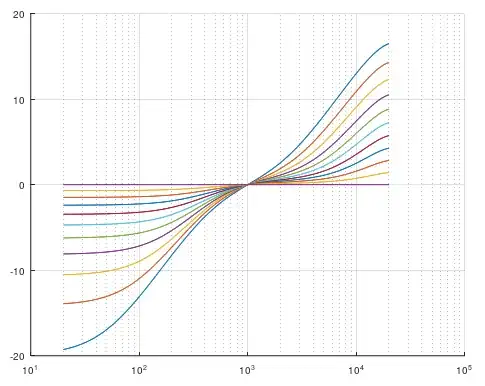
To get flat response in range 20Hz-20kHz you decrease the value of pole1 to around 0.93289462847523175 and pole2 to 0.0. In this example zero1 and zero2 remains untouched. Note: These are not exact values especially for those coefficients from my nor Orban's posts but you get the idea.

Juha

EDIT: Here's Octave code to demonstrate post:

pkg load signal;
pkg load control;
%clear all;
%clf;
Fs = 44100;
minF=20;
maxF=20000; %Fs/2;
sweepF=logspace(log10(minF), log10(maxF),1024);
%% poles for RIAA de-emphasis filter @ 44100
p1 = 0.992894628474;
p2 = 0.739084397546;
z1 = 0.931175652297;
z2 = 0;
%% --------------------------------------------------
RIAApercent = 100                  %% 100 = RIAA, 0 = ~FLAT
%% --------------------------------------------------
RIAApercent = (100-RIAApercent)/100;
k1 = RIAApercent * -0.061718976177;
k2 = RIAApercent * -0.739084397546;
p1 = p1 + k1;
p2 = p2 + k2;
b(1) = 1.0
b(2) = -(p1 + p2)
b(3) = p1 * p2
a(1)= 1.0
a(2)= -(z1 + z2)
a(3)= z1 * z2
%% normalize 0dB @ 1kHz
w = 2.0pi(1000/Fs);
num = b(1)b(1)+b(2)b(2)+b(3)b(3)+2.0(b(1)b(2)+b(2)b(3))cos(w)+2.0b(1)b(3)cos(2.0w);
den = 1.0+a(2)a(2)+a(3)a(3)+2.0(a(2)+a(2)a(3))cos(w)+2.0a(3)cos(2.0*w);
G = sqrt(num/den);
b(1) = b(1)/G;
b(2) = b(2)/G;
b(3) = b(3)/G;
%% plot
hold on;
[h, w] = freqz(a,b, sweepF, Fs);
semilogx(w, 20*log10(h));
grid on;

results:

Reverse the curve by swapping b and a coefficients:

Answer 2

So, sox defines its biquad operation parameters as follows:

biquad b0 b1 b2 a0 a1 a2

Apply a biquad IIR filter with the given coefficients. Where b* and a* are the numerator and denominator coefficients respectively.

See http://en.wikipedia.org/wiki/Digital_biquad_filter (where a0 = 1).

This effect supports the −−plot global option.

A biquad filter is just a special case of an IIR filter, which is a linear system!

That means that you can just have two signal streams, one filtered and one un-filtered, and add them up, scaled by two coefficients with constant sum.

The only thing you'd have to care about is delay, which is a bit tricky to calculate for IIRs; now, luckily, the RIAA biquad guarantees phase errors of this filter to be below 30% at any given frequency, so you can probably get away with summing up with a single-sample delayed input signal.

A single sample delay is a FIR filter with coefficients

b0 = 0, b1 = 1

and any FIR is also understandable as IIR with all aN==0 but a0=1, since IIRs are linear, you can directly modify the coefficients of your biquad by mutliplying them with the aforementioned coefficient and adding 1-coefficient to a0 and b1