Ultrasonic signal detection

Question

I have created a fairly simple TDOA system that uses ultrasonic signals emitted from two speakers to geolocate (relative to the speakers) mobile phones. The two signals are separated by frequency.

The system has the following constraints:

• The signals must be inaudible. To that end we stick to frequencies above 17 kHz. A few people can still hear that, but most can't.
• Sample rate is 44.1 kHz.
• Music will typically be playing, so there is lots of interference at the lower frequencies.
• We don't have control over how well the speakers and microphones work at the upper frequencies, so we've kept our upper limit at around 20 kHz.

The particular signal that I am using is BPSK modulated 13-bit Barker codes because of their good autocorrelation properties. The autocorrelation looks like the following-

When I cross-correlate the expected signal against the received signal in real life, though, what I get typically looks like this-

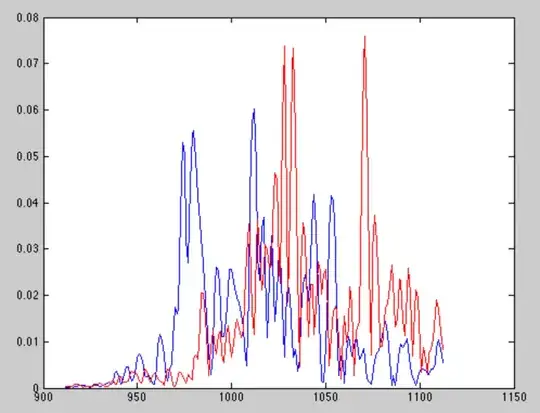
The blue is the cross correlation with the speaker 1 signal, and the red is the cross-correlation with the speaker 2 signal. It appears that the echoes are significant and, unfortunately, often stronger than the direct path signal due to the directional gain of the microphone.

I tried simply detecting the earliest appearance of the signal as that is likely to be the direct path. This approach is very sensitive to the threshold that I use for deciding when the signal is present and so is not robust at all.

I would like a robust approach for determining the "true" arrival time of the signal- i.e. the arrival time of the direct path signal. Perhaps some form of channel estimation and deconvolution? If so, how would that work?

Data/Code: I want to make it clear that I am not expecting anyone to analyze the data or inspect my code. I have made them available in case you want to do so. I am mostly interested in ideas.

I made the raw received signal and modulated expected signals available for download. They are all sampled at 44.1 kHz. Correlating the received signal with the expected signals will produce something similar but not identical to the picture above because I move the received signals to baseband and decimate before correlating with the expected signals.

Received signal

Expected signal #1

Expected signal #2

Matlab scripts The Matlab scripts has both the signal generation script (genLocationSig.m) and my receive/processing script (calcTimingOffset.m).

Answer 1

These are not the codes you are looking for...

As I mentioned in the comments, there are quite a number of ways to do robust TDOA. (Cross-correlation with Linear Chirps, Exponential Chirps, and CDMA-type methods). You have already built a TDOA system utilizing codes, (and that is indeed a good choice over linear-chirps if you need robustness to doppler), however you are limiting yourself artificially in two ways:

• Barker codes only go up to length $13$. We can however make PN-sequence codes of arbitrary length to get a lot more coding gain.
• The use of only $1$ bit in your transmission. We can encode an entire preamble of many bits to transmit, gaining further resilience to multipath.

Use a PN-Sequence:

Thus, very simply, change the codes you use to modulate your carrier by: Use PN-Sequences instead. PN generated codes can be of (nearly) arbitrary length, and can be generated via LFSRs. (They also go by the name 'whiteners' in some texts). Here are three PN-sequences of length $31$, $61$, and $127$ respectively.

PN_31 = [ 1  1 -1 -1  1  1 -1  1 -1 -1  1 -1 -1 -1 -1  1 -1  1 -1  1  1  1 -1  1  1 -1 -1 -1  1  1  1];

PN_61 = [ 1  1  1 -1  1  1 -1  1 -1 -1  1 -1 -1  1  1  1 -1 -1 -1  1 -1  1  1  1  1 -1 -1  1 ...
     -1  1 -1 -1 -1  1  1 -1 -1 -1 -1  1 -1 -1 -1 -1 -1  1  1  1  1  1  1 -1  1 -1  1 -1 ...
      1  1 -1 -1  1  1 -1];

PN_127 = [-1     1     1     1    -1     1    -1    -1     1    -1     1     1    -1    -1    -1     1     1    -1     1     1     1     1    -1     1     1    -1     1    -1 ...
       1     1    -1     1     1    -1    -1     1    -1    -1     1    -1    -1    -1     1     1     1    -1    -1    -1    -1     1    -1     1     1     1     1     1 ...
      -1    -1     1    -1     1    -1     1     1     1    -1    -1     1     1    -1     1    -1    -1    -1     1    -1    -1     1     1     1     1    -1    -1    -1 ...
       1    -1     1    -1    -1    -1    -1     1     1    -1    -1    -1    -1    -1     1    -1    -1    -1    -1    -1    -1     1     1     1     1     1     1     1 ...
      -1     1    -1     1    -1     1    -1    -1     1     1    -1    -1     1     1     1];

The circular and linear auto-correlations of the sequences are shown below. They will clearly yield white spectra, but more than that, we are no longer limited to $13$ chip lengths. In fact, the last code, PN_127, yields a coding gain of $10 \ log [\frac{127}{13} ] \approx 10$ dB gain over the barker sequence, all the while guaranteeing white spectra.

Transmit a preamble:

In your particular application, you mentioned that you were only transmitting one bit. You should try to avoid this if you can help it, and transmit as many bits as your application can allow, to get further coding gain out.

This is what is commonly done on communication protocols to align with the beginning of a packet. A (known) preamble is transmitted, composed of many bits. Each bit, is composed of many chips. (In our example, $31$, $61$, or $127$ chips with either of the above PN codes). Lastly, the bit sequence itself can be composed of yet another PN sequence, or if you like, you may transmit $13$ bits composing a barker pattern, with each bit being composed of either one of the the above PN sequences.

---

Try one or both of those solutions, and put up your results. I expect there to be tangible improvements that we can then iterate on. (Pulse shaping, different/longer PN sequences, etc).