The problem is at least NP-hard, by a reduction from 3-SAT.
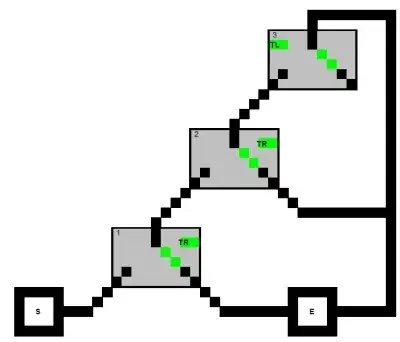
First consider the problem of finding a path from the Start to the Exit of the following directed graph with the restriction that no path may visit all three (square) nodes of a clause:
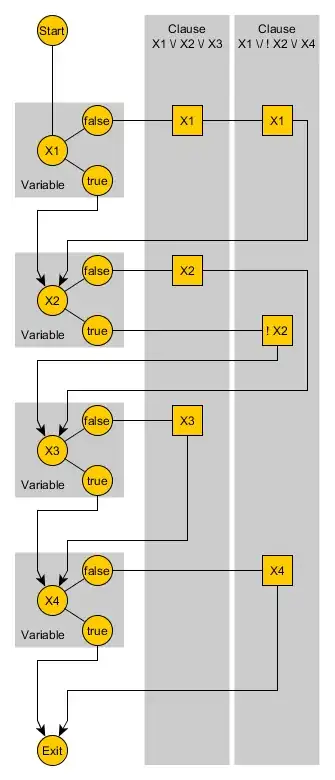
For this graph, such a path only exists if the formula $(X1 \lor X2 \lor X3)\land(X1\lor\neg X2\lor X4)$ can be satisfied. We can build such graphs for arbitrary formulas in 3-CNF, and finding such a path is NP-complete.
We transform these graphs to a switch network. For this we use three gadgets:
- Every circle node and bidirectional edge becomes a Wire, forming the connections between switches.
- Every directed edge becomes a One-way gadget consisting of a single switch (see below).
- Every square node represents one of the three switches that are part of a Clause gadget (see below).
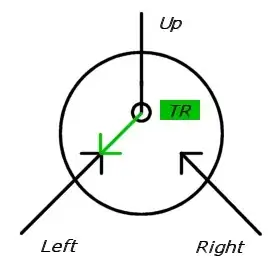
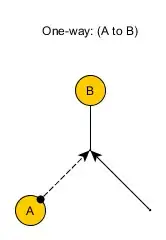
In the following illustrations, switches are drawn as two incoming arrows, one of which is dashed (disabled). The target direction is drawn with a black circle (such that the solid arrow must eventually be on the side of the circle).
Remark: We will use boldface to distinguish the Exit of the graph from exits of gadgets.
For the One-way gadget, entrance $A$ cannot be reached from exit $B$ until $B$ has been reached from $A$.
For the Clause gadget, entrances $X1$, $X2$ and $X3$ lead to exits $X1'$, $X2'$ and $X3'$, respectively.
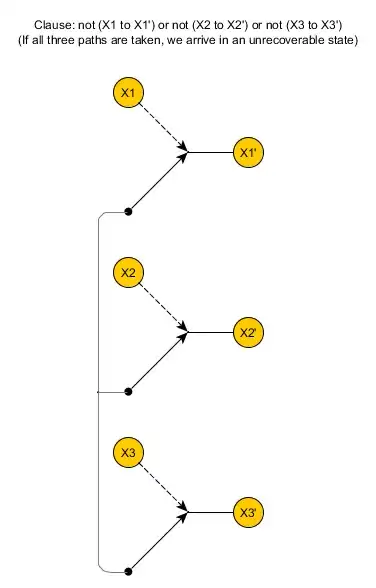
Recall that for the original graph, finding a path that led to the Exit and did not visit all three square nodes of any clause was NP-complete.
Now consider the problem of reaching the Exit of the transformed graph without worrying about the target positions of the switches.
Observe that any path that is a solution for the original graph problem is also a solution for the transformed graph.
So assume a path for the transformed graph is not a solution for the original graph.
This may happen in two cases:
- A One-way gadget is traversed in the unintended direction ($B$ to $A$).
- A path traverses all three paths of some Clause gadget.
In the first case, the One-way gadget must have first been traversed in the intended direction, in which case the path might as well have avoided traversing it in the first place.
So consider the second case where the path traverses all three switches of some Clause gadget.
Then that gadget will have all its three switches flipped (see below). This is where we make use of the target positions.
Notice that the gray backbone of the Clause gadget can no longer be reached, meaning that the switches can no longer be directed to their target positions.
In this case, we say that this Clause gadget is unrecoverable.
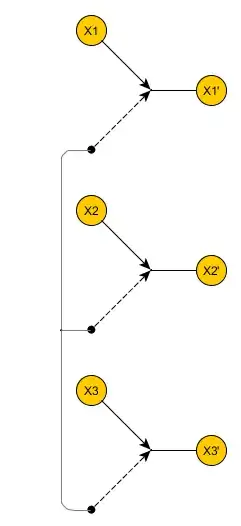
It remains to show that for any solution of the original graph problem, the switches of the transformed graph can be placed in their target position.
For this, we make use of the fact that the Exit wire can only be reached when there is a solution, or some Clause gadget becomes unrecoverable.
To place switches in their target position, we can now add additional One-way gadgets from the Exit wire to the entrance of every existing One-way gadget, as well as to the three exit wires of all Clause gadgets.
Then, once the token reaches the Exit, all the additional One-way gadgets can be traversed (and thereby put in their target position), and also put the remaining switches in their target positions (unless there is an unrecoverable clause).
Finally, the token can return to the Exit and the puzzle is solved.
We should remark that Clause gadgets can only be recovered when entered from an untraversed exit; and due to the One-way gadgets that are placed between Clause gadgets and the next variable, this cannot happen until the Exit wire is reached.
Hence, the switch network problem is NP-hard.
It is still unclear if the problem is in NP or PSPACE-hard.
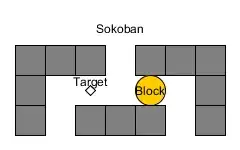
An NP-hardness reduction constructing a planar switch network will have great implications for restricted variants of Sokoban, namely because all switches are equivalent to the Sokoban gadget below.