15

Let G be an n-node undirected graph, and let T be a node subset of V(G) called terminals. A distance preserver of (G,T) is a graph H satisfying the property

$$d_H(u,v) = d_G(u,v)$$

for all nodes u, v in T. (Note that H is NOT necessarily a subgraph of G.)

For example, let G be the following graph (a) and T be the nodes on the external face. Then graph (b) is a distance preserver of (G,T).

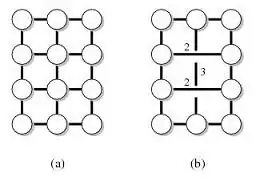
enter image description here

Distance preserver with various parameters are known to exist. I'm particularly interested in the one with the following properties:

  1. G is planar and unweighted (that is, all edges of G has weight one),
  2. T has size $O(n^{0.5})$, and
  3. H has size (the number of nodes and edges) $o(n)$. (It would be nice if we have $O(\frac{n}{\log\log n})$.)

Does such a distance preserver exist?

If one cannot meet the above properties, any kind of relaxations are welcomed.

References:

Distance preserver is also known as an emulator; many related work can be found on internet by searching the term spanner, which requires H to be a subgraph of G. But in my applications we can use other graphs as well, as long as H preserves the distances between T in G.

Glorfindel
  • 359
  • 1
  • 4
  • 10
Hsien-Chih Chang 張顯之
  • 7,638
  • 4
  • 44
  • 83

2 Answers2

5

Many years later, it looks like OP has finally answered his own question: Near-Optimal Distance Emulator for Planar Graphs by Hsien-Chih Chang, Paweł Gawrychowski, Shay Mozes, and Oren Weimann was just posted on the arxiv.

The answer to the original question is yes: it is shown that $\widetilde{O}(\min\{t^2, \sqrt{tn}\})$ edges suffice to preserve distances between $|T| =: t$ terminals, which is optimal up to log factors. In particular $\widetilde{O}(n^{3/4})$ edges suffice for the setting in the OP. This preserver can also be computed in $\widetilde{O}(n)$ time; I would strongly suspect that the log factors in the size can be removed if we care only about existence and not computation time of the preserver, but I have not rigorously verified this.

(On a less formal note, I find this result really amazing. Congrats!)

GMB
  • 2,393
  • 15
  • 20
  • 1
    Thank you @GMB for posting it as an answer. A small catch here is that the preserver is directed; it is an open question whether an undirected (but still not necessarily planar) emulator of sublinear-size exists. But it is quite satisfying to finally know the answer to an old question after all these years :) – Hsien-Chih Chang 張顯之 Jul 05 '18 at 16:29
2

you may want to look at Klein's planar subset spanner, which preserves distances up to a 1+epsilon factor.

A Subset Spanner for Planar Graphs, with Application to Subset TSP http://doi.acm.org/10.1145/1132516.1132620

Christian Sommer
  • 761
  • 6
  • 7
  • Thanks, I've read the paper, and there's a gap between his construction and our requirements. It seems that any spanner won't work as long as it is a subgraph of the original graph; one can take a grid graph as a counter-example. But there are emulators for the grid graphs. – Hsien-Chih Chang 張顯之 Apr 25 '11 at 02:50
  • another construction idea, maybe it works?

    1. recursively apply shortest-path separators (Thorup, FOCS'01)

    2. eps-cover for each vertex

    [first two steps construct distance labels] there are sqrt{n} terminals, each with a label of size O(log n / eps), connecting to a total number of at most sqrt{n}*log n paths and 1/eps times more portals

    1. shortcut the portals on paths by weighted edges and shortcut the connections to portals by edges

    the resulting graph should have roughly sqrt{n}*log n vertices and edges (up to eps) and represent 1+eps shortest paths

    for exact distances I don't know...

     – Christian Sommer Apr 26 '12 at 00:33