Reading Baier and Katoen closely, they are considering both finite and infinite transition systems. See page 20 of that book for definitions.
First, take the simple transition system $EVEN$:
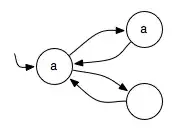
Lemma: No LTL formula recognizes the language $L_{even} = $Traces$(EVEN)$. A string $c \in L_{even}$ iff $c_i = a$ for even $i$. See Wolper '81. You can prove this by first showing that no LTL formula with $n$ "next-time" operators can distinguish the strings of the form $p^i\neg p p^\omega$ for $i> n$, by a simple induction.
Consider the following (infinite, non-deterministic) transition system $NOTEVEN$. Note that there are two different initial states:
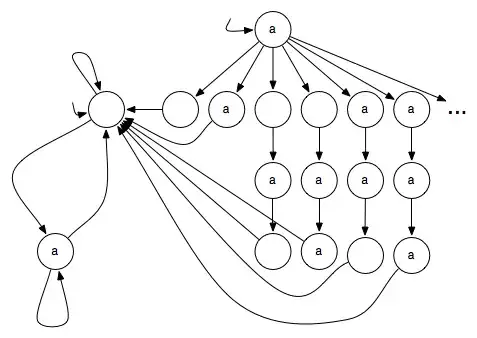
Its traces are precisely $\{a,\neg a\}^\omega - L_{even}$.
Corollary to the Lemma: If $NOTEVEN \vDash \phi$ then $EVEN \not\vDash \neg\phi$
Now, consider this simple transition system $TOTAL$:
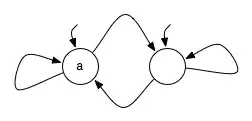
Its traces are clearly $\{a,\neg a\}^\omega$.
Thus, $NOTEVEN$ and $TOTAL$ are not trace equivalent. Suppose they were LTL inequivalent. Then we would have an LTL formula $\phi$ such that $NOTEVEN \vDash \phi$ and $TOTAL \not\vDash \phi$. But then, $EVEN\vDash \neg\phi$. This is a contradiction.
Thanks to Sylvain for catching a stupid bug in the first version of this answer.


