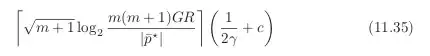Deciding whether a convex region is empty

Question

Let $S\subseteq \mathbb{R}^n$ be a convex region defined by $$g_i(x)\leq 0, ~~i\in 1,\ldots,m,$$ where $g_i$ are convex functions. The goal is to decide whether $S$ is empty, and if not - find a point $x\in S$.

In the book of Boyd and Vandenberghe (chapter 11), I found the following algorithm. Solve the following optimization problem:

$$\text{ mininize } ~~p~~ \text{ subject to } ~~g_i(x)\leq p, ~~i\in 1,\ldots,m.$$

Denote the optimal solution by $(p^*,x^*)$. If $p^*>0$, then $S$ is empty. If $p^*\leq 0$, then $x^*$ is a point in $S$ (in particular, if $p^* < 0$ then $x^*$ is in the interior of $S$; if $p^*=0$ then interior of $S$ is empty and $x^*$ is a boundary point).

The problem is that, when $p^*$ approaches 0, the runtime complexity of solving this auxiliary problem approaches infinity; here is the exact runtime from the book of Boyd and Vandenberghe:

As you can see, $p^*$ is in the denominator. They also say that:

I would like to know what is known about the complexity of this decision problem. In particular:

• Suppose the functions $g_i$ are given explicitly (e.g. they are all polynomials with rational coefficients; this also means that they are continuously differentiable infinitely many times), and every basic arithmetic operation on real numbers takes unit time. Is there a proof that the decision problem cannot be solved in a finite number of arithmetic operations?
• Are there sub-classes of convex functions (except linear functions) for which the decision problem can be solved in finite time? In polynomial time?

EDIT: Based on the comments, it seems the question is non-trivial even in the case of quadratic programming, where all functions $g_i$ are convex quadratic functions. The Wikipedia page mentions that the problem can be solved in weakly-polynomial time using the ellipsoid method, but to use the ellipsoid method we need a lower bound on the volume of the feasible region, which is not always guaranteed.

Answer 1

Warning: As one of the comments points out, the sum of squares is not necessarily convex, so the hardness reduction suggested below does not work. The problem still lies in $\exists\mathbb{R} \subseteq \mathrm{PSPACE}$ though.

Deciding whether there is an $x \in \mathbb{R}^n$ such that $f_i(x) = 0$ for a family of quadratic polynomials is complete for the existential theory of the reals, $\exists\mathbb{R}$. So testing whether $f(x) = \sum_i (f_i(x))^2 \leq 0$ has a solution is also complete for $\exists\mathbb{R}$, and, as a sum of squares, $f$ is a convex function. So solving the non-emptiness problem of a convex set is as hard as deciding truth in the existential theory of the reals.

The hardness result goes back to Blum, Shub, and Smale. On a Theory of Complexity over the Real Numbers, it follows from the main theorem, but it's stated in the BSS-model. A statement in the $\exists\mathbb{R}$-framework can be found as Lemma 3.2 in Schaefer, Stefankovic. Fixed Points, Nash Equilibria, and the Existential Theory of the Reals.