20

A colleague who works on genetic programming asked me the following question. I first tried to solve it based on a greedy approach, but on a second thought, I found a counterexample to the greedy algorithm. So, I thought it's worth mentioning here.

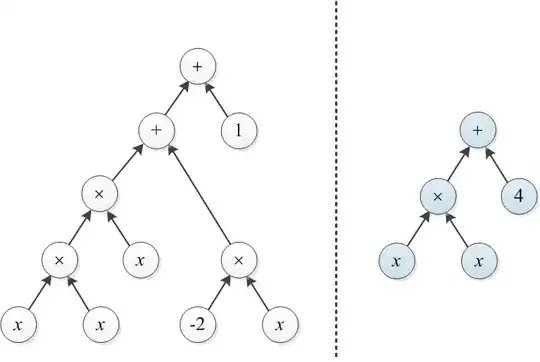
Consider two polynomials which are represented by their expression trees. For instance, $x^3-2x+1$ and $x^2 + 4$ are illustrated below:

Rules:

  1. Each node is either a variable name ($x, y, z, \ldots$), a number, or an operation (+,-,×).
  2. The in-order traversal of the tree should result in a valid polynomial.
  3. Operation nodes have in-degree 2. Other nodes have in-degree 0. All nodes have out-degree 1 (except root, whose out-degree is 0).

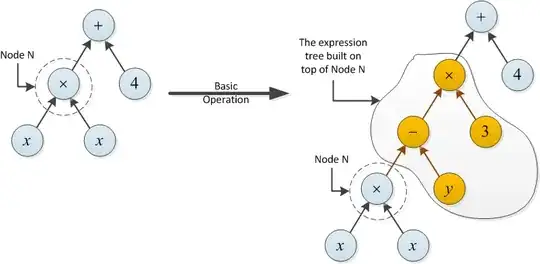
On a node N of the tree, define the basic operation as follows:

  1. A basic operation can change the label of the node. For instance, $x$ can be changed to 3, or + can be changed to $\times$.
  2. A basic operation can build an expression tree on top of N (see the example below).

The cost of the basic operation of type 1 is 1. The cost for type 2 is equal to the number of {+,-,×} operations in the newly built expression tree.

Example for type 2: The cost of the following basic operation is 2, since the expression tree built on top of node N uses two operations (- and ×).

Let T1 and T2 be two expression trees representing polynomials. Define the distance of T1 and T2 as follows: the minimum cost of basic operations for converting T1 to T2. Note that we don't require the converted tree to have the same structure as T2. We just want it to compute the same polynomial as T2. (See the comments for an example.)

The problem: Given T1 and T2, present an algorithm which computes their distance.

Example 1: Let T1 and T2 are the two trees illustrated at the beginning of this post. To convert the right tree to the left tree, one can build a tree of cost 3 on top of ×, and change 4 to 1 (the total cost is 4).

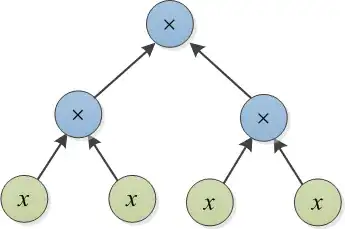
Example 2: Let T1=$x^4$ be represented by the following tree. To convert T1 to T2=$x^4+4x^3+6x^2+4x+1$, it suffices to add 1 to each of the $x$ nodes, to optain $(x+1)^4$=T2. This can be done by adding a cost-1 expression tree on top of each $x$ node. This example shows that the term-by-term conversion (which I called the greedy approach at the beginning of this post) is not an optimal approach. That is, if one wants to produce terms in T2 which are not present in T1 (i.e. $4x^3$, $6x^2$, $4x$, and 1), the cost will be much higher.

Glorfindel
  • 359
  • 1
  • 4
  • 10
Sadeq Dousti
  • 16,479
  • 9
  • 69
  • 152
  • 2
    If "delete" operation is not allowed, then the distance is not a distance. For example: a tree T1=(xx)+4 cannot be transformed to T2=x, but T2 can be transformed to T1 adding (x) and then (+4) on top of x. Is it ok ? Or you should define the distance as the minum operations required to convert T1 to T2 or T2 to T1. – Marzio De Biasi Feb 06 '11 at 11:43
  • 1
    Very well posed question, might serve as an example in our FAQ. Any particular reason why nodes can not be expanded, say $x \mapsto \times(x, x)$, or reduced, say $x \mapsto \times(x, x)$? – Raphael Feb 06 '11 at 12:09
  • @Vor: In the example you provided ($x \times x + 4$), the relabeling works: change the label of one of the $x$ nodes to 1. You obtain $1 \times x + 4 = x + 4$. Then change the label of 4 to 0, you obtain: $x$. Correct? – Sadeq Dousti Feb 06 '11 at 12:12
  • @Raphael: Thanks for your opinion about the question :) I didn't understand the difference between expansion and reduction, because the examples you provided were identical: $x \mapsto \times(x, x)$. I think it's a typo, right? – Sadeq Dousti Feb 06 '11 at 12:15
  • 1
    Indeed, I intended to turn it around. :> As for $1 \times x + 4 = x + 4$, this is algebraically clear, but you have indeed no operation that transforms from left to right. Or do we not need to have the same tree at the end, but only an equivalent one? – Raphael Feb 06 '11 at 12:37
  • @Raphael: You're right. I should have mentioned that we only require the trees to be equivalent. I'll correct this in the body of the question. – Sadeq Dousti Feb 06 '11 at 14:21
  • The second example doesn't seem to be the same as the problem statement: are the inputs trees or polynomials? – Peter Taylor Feb 06 '11 at 14:23
  • @Peter: The inputs are polynomials, but they are represented as trees. I'll change the subject of this post to clarify it. (Also, note the problem statement: Given T1 and T2,...) – Sadeq Dousti Feb 06 '11 at 14:26
  • @Sadeq, my point was that the problem statement talks about trees, the first example has two trees as input, but the second example appears to have one tree and one polynomial as input. – Peter Taylor Feb 06 '11 at 14:30
  • @Peter: You're totally right. It seems that I was too lazy to draw the polynomial for $x^4+4x^3+6x^2+4x+1$. Just try to consider the most natural case, since it will occupy a lot of the page if I try to illustrate it. In Polish notation, it will be $+(+(+(+(\times(\times(x,x),\times(x,x)),\times(4,\times(x,\times(x,x)))),\times(6,\times(x,x))),\times(4,x)),1)$. – Sadeq Dousti Feb 06 '11 at 14:56
  • Can't really answer, but +1 for the gorgeous diagramming (also, the nice question ;) – Agos Feb 06 '11 at 17:06
  • 1
    If I am not mistaken, even deciding whether the cost is 0 or not is not known to be in deterministic polynomial time (but is known to be in randomized polynomial time). – Tsuyoshi Ito Feb 06 '11 at 17:59
  • @Tsuyoshi: Could you please elaborate? – Sadeq Dousti Feb 06 '11 at 19:05
  • 4
    The cost is equal to 0 if and only if the two given (division-free) arithmetic formulas represent the same polynomial. If I remember it correctly, this is a typical problem in coRP (by random assignment) which is not known to be in P. – Tsuyoshi Ito Feb 06 '11 at 19:06
  • 4
    @Tsuyoshi: Oh, I see. You're pointing at the polynomial identity testing problem. (Good references: [1] and [2]). I must think about this. Meanwhile, any suggestion is welcome. – Sadeq Dousti Feb 06 '11 at 19:56
  • 4
    Yes, that’s it. It seems that in the typical version of the polynomial identity testing problem, two input polynomials are given as circuits, not formulas. So my wording that the formula version is “typical” was probably inaccurate. Anyway putting even the formula version in P seems to be an open problem. – Tsuyoshi Ito Feb 06 '11 at 20:08
  • @Tsuyoshi: I have yet to talk to my colleague about this issue, but I think it'll be no problem: We can still compare the polynomial trees in poly-time with enough accuracy, and that's enough for the genetic programming (I guess). – Sadeq Dousti Feb 06 '11 at 20:57
  • 1
    Well, my point is that we cannot hope for a deterministic polynomial-time exact algorithm for the problem. I do not rule out the possibility that there may be a randomized algorithm or a deterministic approximate algorithm (with respect to a suitable approximation measure), but to find them, we have to be aware that we need something other than the most basic kind of algorithm, that is, a deterministic poly-time exact algorithm. – Tsuyoshi Ito Feb 06 '11 at 21:04
  • @Sadeq in your question you talk about "trees" (T1, T2) so I thought that both T1 and T2 were fixed, in this case x+0 != x (they are different trees, even if they represent the same polynomial). However I see that the focus is on the polynomial identity testing problem. – Marzio De Biasi Feb 06 '11 at 21:44
  • In fact, we have problems just figuring out wether or not we can terminate (i.e. wether what we have is equivalent tot he target), let alone figure out good steps. – Raphael Feb 07 '11 at 01:16
  • 2
    @Vor: In the current formulation, the input T1 is really a tree and the input T2 is a polynomial which just happens to be given as a tree, in the following sense. Changing T1 to a different tree which represents the same polynomial can change the answer in general, whereas changing T2 in a similar way does not. – Tsuyoshi Ito Feb 07 '11 at 02:08
  • Anyone reading this who just wants to import a library should have a look at APTED. Open source Java, MIT licence, reasonable fast. Most other languages have ways of integrating with Java. – AnnanFay May 07 '18 at 02:13
  • Have you considered using a "Tree Edit Distance" algorithm? – Aviv Feb 06 '11 at 15:57
  • Do you mean this algorithm? – Sadeq Dousti Feb 06 '11 at 16:47

1 Answers1

10

Tree Edit Distance is a generalization of string edit distance. The distance between two trees is the minimum number of node insertions \ deletions \ and relabels required to turn one tree into the other. (when we delete node v, v's children become children of parent(v)). The problem is NP-hard when the trees are unordered, but when they are ordered (i.e., there is a left-to-right order among siblings) the problem is solvable in O(n^3) time (as in the paper that Sadeq mentioned). A good survey that describes this: http://portal.acm.org/citation.cfm?id=1085283

Aviv
  • 116
  • 1
  • 2