A simple path is a path that doesn't revisit a node. A simple cycle is a cycle that doesn't revisit an edge. You are given an undirected graph G which may contain edges of negative weight but which will not contain any simple cycles of negative weight. Is there an efficient algorithm for finding the minimum weight simple path between any two nodes of G?
Notes:
Without the no-negative-simple-cycle constraint, this problem is NP-Hard.
The reason I'm interested in this problem is because the weight of the min-weight simple path should be a good estimate of the "safety level" of the syndrome extracted during quantum error correction. In this case the edges of the graph correspond to physical error mechanisms, the negative edges are the physical errors that are part of the extracted syndrome, the no-negative-cycles property is guaranteed by the fact that the syndrome extraction would have used any such cycle to produce a better syndrome, and a simple path between two particular nodes can be multiplied into a syndrome to get a different syndrome that disagrees about the logical correction to make.
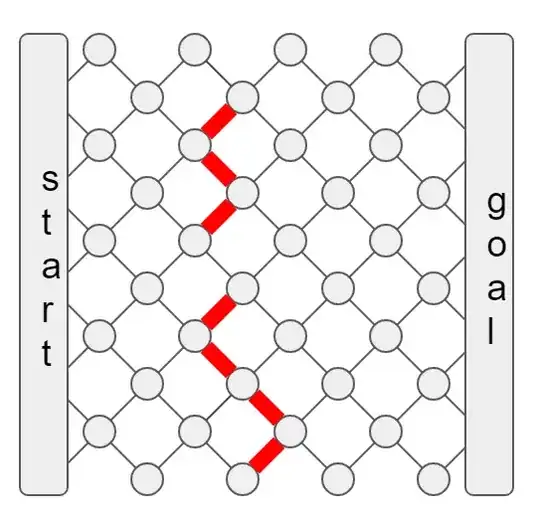
I initially thought that the Bellman-Ford algorithm would work, after tweaking it so that each node refused to backtrack to its current predecessor. However, this can create deadlock situations where the optimal solution is to detour through multiple beneficial regions but the local greedy checks can't see past the initial cost of entering into a beneficial region. For example, in the graph below where you're trying to path from left to right, the optimal solution is to move vertically through almost all the negative edges (in red). Bellman-Ford can fail to find this solution, depending on the order in which the search progresses: