16

Given $n$ inputs $x_0, \ldots, x_{n-1}$, we construct a random sorting network with $m$ gates by iteratively picking two variables $x_i, x_j$ with $i < j$ and adding a comparator gate that swaps them if $x_i > x_j$.

Question 1: For fixed $n$, how large must $m$ be for the network to correctly sort with probability $> \frac{1}{2}$?

We have at least the lower bound $m = \Omega(n^2 \log n)$ since an input that is correctly sorted except that each consecutive pair is swapped will take $\Theta(n^2 \log n^2)$ time for each pair to be chosen as a comparator. Is that also the upper bound, possibly with more $\log n$ factors?

Question 2: Is there a distribution of comparator gates that achieves $m = \tilde{O}(n)$, perhaps by choosing close comparators with higher probability?

Geoffrey Irving
  • 3,253
  • 15
  • 29
  • 1
    I guess one can get a $O(n^3log^{O(1)})$ upper bound by looking at one input at a time and then union bounding, but that sounds far from tight. – daniello Feb 28 '18 at 21:13
  • 2
    Idea for Question 2: pick a sorting network of depth $O(\log^2 n)$. At each step, randomly pick one of the gates of the sorting network, and perform that comparison. After $\tilde{O}(n)$ steps, all gates in the first layer will have been applied. After another $\tilde{O}(n)$ steps, all gates in the second layer will have been applied. If you can show that this is monotonic (inserting extra comparisons in the middle of the sorting network can't hurt), you'll have obtained a solution with $\tilde{O}(n)$ comparators in total on average. I'm not sure whether monoticity actually holds, though. – D.W. Feb 28 '18 at 21:42
  • @D.W.: And if that argument works for bitonic sort, you can replace the sorting network with a distribution where the probability $p_k$ of picking a comparator of length $k$ is proportional to $1/\lg k$ for $k$ a power of two and zero otherwise. – Geoffrey Irving Feb 28 '18 at 23:01
  • Do you require that the network correctly sorts every input of length n? Or is your probability dependent on the way in which you generate a random length-n input?

    We can assume all elements are unique and can be mapped to 1...n because if they aren't then the problem is strictly easier. But do you have any other constraint on the input?

     – Phylliida Mar 01 '18 at 23:40
  • 1
    It has to sort every input, but since it's a sorting network that is equivalent to sorting every bit sequence. – Geoffrey Irving Mar 01 '18 at 23:47
  • 2
    @D.W.: Monotonicity doesn't necessarily hold. Consider sequences $$\begin{eqnarray} s &=&(x_1, x_2), (x_0, x_2), (x_0, x_1);\ s'&=&(x_1, x_2), \mathbf{(x_0, x_1)}, (x_0, x_2), (x_0, x_1).\end{eqnarray}$$ Sequence $s$ works; $s'$ doesn't (consider input (1, 0, 0)). The idea is that $(x_0, x_2), (x_0, x_1)$ sorts any input it receives except $(0, 1, 0)$ (see here). In $s$, that input cannot reach $(x_0, x_2), (x_0, x_1)$. In $s'$ it can. – Neal Young Mar 03 '18 at 23:57
  • 3
    Consider the variant where the network is chosen by picking two adjacent variables $x_i, x_{i+1}$ randomly at each step. Now monotonicity holds (as adjacent swaps don't create inversions). Apply @D.W.'s idea to an odd-even sorting network, which has $n$ rounds: in odd rounds it compares all adjacent pairs where $i$ is odd, in even rounds it compares all adjacent pairs where $i$ is even. W.h.p. the random network is correct in $O(n^2\log n)$ comparisons, as it "includes" this network. (Or am I missing something?) – Neal Young Mar 04 '18 at 03:26
  • @Neal: Seems like that would be provable by tracking the number of inversions if $k$ inversions implies at least $k/n$ adjacent flips. – Geoffrey Irving Mar 04 '18 at 04:12
  • You can have $\Omega(n^2)$ inversions with just 1 adjacent flip (e.g.: 4,5,6,7,8,1,2,3,4). But I think it's provable as outlined in my comment: it takes $O(n\log n)$ random adjacent comparisons (w.h.p.) to do all odd (or all even) adjacent comparisons. So you cover one round of the odd-even network in $O(n\log n)$ comparisons, and you cover all $n$ rounds in $O(n^2\log n)$ comparisons. Then by monotonicity you are done. (Or am I missing something?) – Neal Young Mar 04 '18 at 04:28
  • @NealYoung: Yes, that works. I don't see the easy proof that monotonicity holds for all adjacent networks (though I expect it exists), but odd-even sort plus extra gates certainly takes only $O(n)$ passes. – Geoffrey Irving Mar 04 '18 at 06:07
  • 2
    Monotonicity of adjacent networks: Given $a, b\in{0,1}^n$, for $j\in{0,1,\ldots,n}$ define $s_j(a) = \sum_{i=1}^j a_i$. Say $a\preceq b$ if $s_j(a) \le s_j(b)$ ($\forall j$). Fix any comparison "$x_i < x_{i+1}$". Let $a'$ and $b'$ come from $a$ and $b$ by doing that comparison. Claim 1. $a' \preceq a$ and $b' \preceq b$. Claim 2: if $a\preceq b$, then $a' \preceq b'$.
    Then show inductively: if $y$ is the result of comparison sequence $s$ on input $x$, and $y'$ is the result of super-sequence $s'$ of $s$ on $x$, then $y' \preceq y$. So if $y$ is sorted, so is $y'$.     – Neal Young Mar 04 '18 at 16:23
  • 1
    FWIW I think that monotonicity of the odd-even network holds w.r.t.. arbitrary (even non-adjacent) comparisons, in that adding arbitrary comparisons won't break it. The correctness of the odd-even network follows from an invariant similar to (but not quite) the following: after $2t$ rounds (of adjacent odd/even comparisons), the $i$th smallest is in position $\le n + 2i-t$ from the top. (This invariant is "universal" in the sense that it is independent of the input.) I believe the invariant is maintained even if arbitrary additional comparisons (adjacent or not) are interspersed. – Neal Young Mar 06 '18 at 03:44
  • @NealYoung: Want to upgrade that to an answer? I think it fully resolves question 1. – Geoffrey Irving Mar 06 '18 at 04:12
  • Does it resolve Question 1? If you choose arbitrary comparisons at random, won't it take $m=\Theta(n^3 \log n)$ comparisons to dominate the odd-even network? This would be similar to Daniello's suggested bound of $O(n^3\log^{O(1)} n)$. But the right answer is more like $O(n^2\log n)$, probably? – Neal Young Mar 06 '18 at 13:19
  • @NealYoung: Apologies, you’re right that it’s cubic. And experiments similar to below do show approximate quadratic behavior (not sure about log factors). – Geoffrey Irving Mar 06 '18 at 15:23

1 Answers1

3

Here's some empirical data for question 2, based on D.W.'s idea applied to bitonic sort. For $n$ variables, choose $j - i = 2^k$ with probability proportional to $\lg n - k$, then select $i$ uniformly at random to get a comparator $(i,j)$. This matches the distribution of comparators in bitonic sort if $n$ is a power of 2, and approximates it otherwise.

For a given infinite sequence of gates pulled from this distribution, we can approximate the number of gates required to get a sorting network by sorting many random bit sequences. Here's that estimate for $n < 200$ taking the mean over $100$ gate sequences with $6400$ bit sequences used to approximate the count: 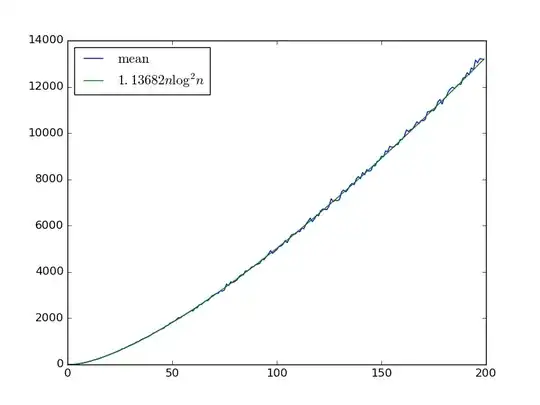Approximate number of gates It appears to match $\Theta(n \log^2 n)$, the same complexity as bitonic sort. If so, we don't eat an extra $\log n$ factor due to the coupon collector problem of coming across each gate.

To emphasize: I'm using only $6400$ bit sequences to approximate the expected number of gates, not $2^n$. The mean required gates does rise with that number: for $n = 199$ if I use $6400$, $64000$, and $ 640000$ sequences the estimates are $14270 \pm 1069$, $14353 \pm 1013$, and $14539 \pm 965$. Thus, it's possible getting the last few sequences increases the asymptotic complexity, though intuitively it feels unlikely.

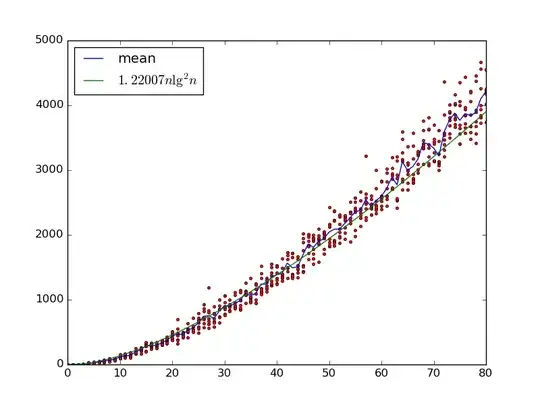
Edit: Here's a similar plot up to $n = 80$, but using the exact number of gates (computed via a combination of sampling and Z3). I've switched from power of two $d = j-i$ to arbitrary $d \in [1,\frac{n}{2}]$ with probability proportional to $\frac{\log n - \log d}{d}$. $\Theta(n \log^2 n)$ still looks plausible.

Exact numbers of gates

Geoffrey Irving
  • 3,253
  • 15
  • 29
  • 3
    Nice experiment! There's a different way the coupon collector issue could arise here, though: you're only sampling a small fraction of the $2^n$ bit sequences needed to verify correctness on all inputs. It seems we can conclude (scientifically, not mathematically of course) from your experiment that a random network of this type and size sorts a random permutation whp. I'd also be curious to see exhaustive $2^n$ testing on such random networks for all $n$ up to which you're willing to go. ($n=20$ shouldn't be too bad, maybe even $n=30$ depending on what language & hardware you're using). – Joshua Grochow Mar 05 '18 at 14:46
  • 1
    It looks the same for exact up to $n = 27$, but I don’t view that as conclusive. – Geoffrey Irving Mar 05 '18 at 15:28
  • 1
    @JoshuaGrochow: I've added exact values up to $n = 80$. – Geoffrey Irving Mar 06 '18 at 08:02
  • 1
    Nice! There does appear to be a growing spread to the exact data though, which perhaps indicates an upper bound with an extra factor of $\log n$? (That is, if the "spread" is growing at a rate of $\log n$.) – Joshua Grochow Mar 06 '18 at 17:53
  • 1
    Yeah, we can't rule out an extra factor. I'd be surprised if it was $\log n$, though, since up at 80 we have $\lg n \approx 6$ and the constant is suspiciously close to $1$ otherwise. At this point I think theory has to take over. :) – Geoffrey Irving Mar 06 '18 at 18:14
  • Given a network it should be possible to polynomialy determine if it is a sorting network without sampling inputs. – Meir Maor Mar 11 '18 at 06:57
  • Meir: No, see http://larc.unt.edu/ian/pubs/snverify.pdf. – Geoffrey Irving Mar 11 '18 at 14:57