6

Note $S_n$ the Sierpiński sieve graph of order $n$, which is obtained from the connectivity of the Sierpiński sieve.

S_n

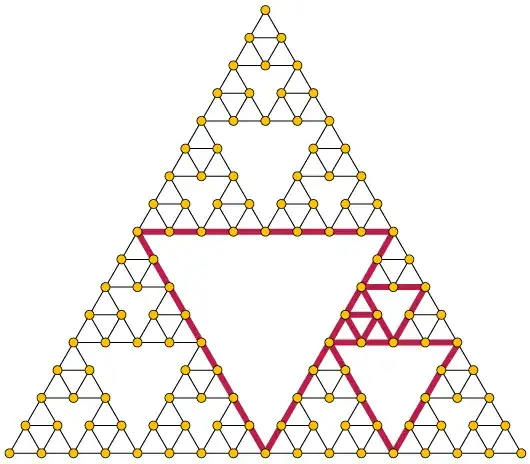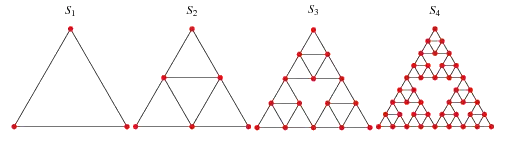
For $n$ high enough, what is the treewidth of $S_n$?

I think that I can show that it is at least $4$ (by obtaining $K_5$ as a graph minor), and that it is at most $5$ (by obtained a tree-decomposition scheme involving bags of size $6$). My gut feeling is that it should be $5$, but I cannot find a proper database for forbidden minors at treewidth $4$ (and I can't access Sanders' thesis mentioned here).

Glorfindel
  • 359
  • 1
  • 4
  • 10
while False
  • 63
  • 2

1 Answers1

17

You can recursively decompose each triangle into a smaller triangle and a trapezoid, and each trapezoid into two smaller triangles. The corresponding tree decomposition (whose bags contain the corners of a triangle at one level of the decomposition and a triangle or trapezoid at the next or previous level) has five vertices per bag and therefore has width four.

There is no $K_5$ minor, because the graph is planar. There is, however, a $K_{2,2,2}$ (octahedron) minor (actually, a subdivision), shown below. As this is one of the forbidden minors for treewidth three, the width is four.

enter image description here

David Eppstein
  • 50,990
  • 3
  • 170
  • 278