12

Again an edge-partitioning problem whose complexity I'm curious about, motivated by a previous question of mine.

Input: a cubic graph $G=(V,E)$

Question: is there a partition of $E$ into $E_1, E_2, \ldots, E_s$, such that the subgraph induced by each $E_i$ is either a claw (i.e. $K_{1,3}$, often called a star) or a $3$-path (i.e. $P_4$)?

I think I saw a paper one day where this problem was proven to be NP-complete, but I cannot find it anymore, and I don't remember whether that result applied to cubic graphs. On a related matter, I'm aware that edge-partitioning a bipartite graph into claws is NP-complete (see Dyer and Frieze). Does anyone have a reference for the problem I describe, or something related (i.e. the same problem on another graph class, that I could then try to reduce to cubic graphs)?

Community
  • 1
Anthony Labarre
  • 3,264
  • 1
  • 25
  • 33
  • 2
    This may help you: Edge Partition into $K_3$ and $K_{1,3}$ is $NP$-Complete. – Mohammad Al-Turkistany Nov 08 '10 at 20:03
  • turkistany, could you add a reference for that to your comment? – Anthony Labarre Nov 08 '10 at 20:15
  • 1
    Anthony, Here is the link (http://www.andrew.cmu.edu/user/jblocki/K-Anonymity.pdf) – Mohammad Al-Turkistany Nov 08 '10 at 20:28
  • Oh, right. That's the paper I remembered, which I wrongly thought tackled exactly my problem. Well, thanks anyway for the reminder, maybe I can indeed do something with it... – Anthony Labarre Nov 08 '10 at 20:41
  • 1
    Do you have an example of a cubic graph that cannot be partitioned in this way? – David Eppstein Nov 09 '10 at 16:39
  • No. I'm currently trying to find such counterexamples using Meringer's list (http://www.mathe2.uni-bayreuth.de/markus/reggraphs.html), but haven't implemented anything to automate that verification yet. – Anthony Labarre Nov 09 '10 at 17:18
  • @Anthony, is $s$ part of the input, or is it fixed, or are you simply wanting to know if a partition exists (for some $s$) as David suggests? – András Salamon Nov 09 '10 at 17:55
  • What do you mean by the subgraph induced by a set of edges? Is it simply the graph formed by the set of edges together with all the endpoints of the edges in the set? – Tsuyoshi Ito Nov 09 '10 at 21:02
  • András: since both kinds of subgraph have exactly three edges, s can only be m/3 = n/2. – David Eppstein Nov 09 '10 at 22:48
  • Tsuyoshi: yes, this is what I meant. András: see David's reply. And I'm interested in obtaining an actual partition, not just knowing that I can get one. – Anthony Labarre Nov 10 '10 at 08:22
  • 2
    The link by @MohammadAl-Turkistany above is dead, but fortunately Wayback machine has it: https://web.archive.org/web/20150414064939/https://www.andrew.cmu.edu/user/jblocki/K-Anonymity.pdf – a3nm Jan 24 '24 at 20:54

3 Answers3

15

This isn't an answer to the complexity of the problem, but it at least shows that the complexity has a chance at being nontrivial: it's an example of a cubic graph that cannot be partitioned into paths and claws.

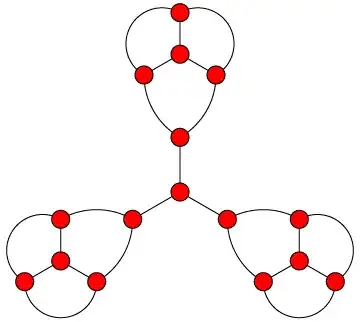
alt text
(source: uci.edu)

Within each of its three lobes, any partition into paths and claws can only use six of the seven edges. The remaining six central edges take the form of a claw with each edge subdivided, which cannot be partitioned into paths and claws.

ETA: The graph shown above is more famous as an example of a cubic graph without a perfect matching. But every cubic graph with a perfect matching has a decomposition into paths (not even using any claws). By König's theorem this includes all cubic bipartite graphs and by Petersen's theorem this includes all bridgeless cubic graphs, answering a question of Joseph Malkevitch in the comments.

The proof is very simple: if M is a perfect matching in a cubic graph, the removal of M leaves a 2-regular graph, that is, a disjoint union of cycles. Orient each cycle arbitrarily, and attach each edge uv of M to the cycle edges that follow u and v in the orientations of their cycles.

In the other direction, if there exists a decomposition into paths, then there exists a perfect matching: the middle edges of each path must be a matching since no two middle edges can share a degree-three vertex.

(Disclaimer: this idea may have already been present in Carsten Thomassen's invited talk at GD 2010, which was about this sort of graph decomposition problem.)

(addition to disclaimer (by Anthony Labarre): the "orientation idea" for going from a perfect matching to a partition into paths appears in this paper by Jünger, Reinelt and Pulleyblank, who attribute it to W. H. Cunningham.)

Glorfindel
  • 359
  • 1
  • 4
  • 10
David Eppstein
  • 50,990
  • 3
  • 170
  • 278
9

It seems I had missed this other paper by Dyer and Frieze, where they prove that partitioning the edges of a planar bipartite graph into connected components with $k$ edges is NP-complete for any fixed $k\geq 3$ (Theorem 3.1 p. 145). They then comment that the problem can be shown to remain NP-complete for $k=3$ if all vertices have degree $2$ or $3$, which unless I parsed this the wrong way includes my problem (since the input is bipartite, the graph contains no odd cycle and in particular no triangle, which means that the only subgraphs we can use are claws and paths).

This wasn't actually the end of the story: if the cubic graph is bipartite, then it's easy to partition its edge set using only claws, by selecting one set of the bipartition and making it a set of "claw centers". The general problem is indeed hard, which can be proved using a reduction from CUBIC PLANAR MONOTONE 1-IN-3 SATISFIABILITY. All details are freely accessible on arxiv.

Anthony Labarre
  • 3,264
  • 1
  • 25
  • 33
6

Perhaps this paper may be of interest:

Kleinschmidt, Peter Regular partitions of regular graphs. Canad. Math. Bull. 21 (1978), no. 2, 177–181.

It deals with graphs which can be written as the union of "Z-paths" of length 3. (Specifically, planar, 3-valent, 3-connected graphs-cubic 3-polytopes.)

Joseph Malkevitch
  • 1,319
  • 6
  • 7