Avalanche like stochastic process

Question

Consider the following process:

There are $n$ bins arranged from top to bottom. Initially, each bin contains one ball. In every step, we

1. pick a ball $b$ uniformly at random and
2. move all the balls from the bin containing $b$ to the bin below it. If it already was the lowest bin, we remove the balls from the process.

How many steps does it take in expectation until the process terminates, i.e., until all $n$ balls have been removed from the process? Has this been studied before? Does the answer follow easily from known techniques?

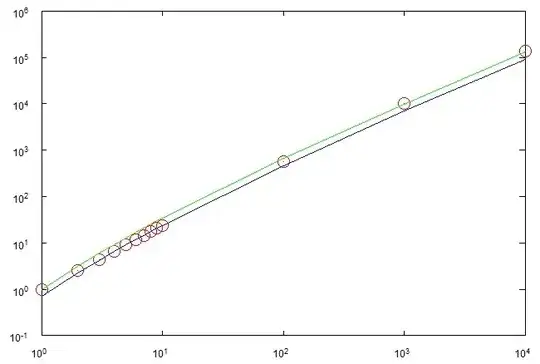
In the best case, the process can finish after $n$ steps. In the worst case it can take $\Theta(n^2)$ steps. Both cases should be very unlikely though. My conjecture is that it takes $\Theta(n\log n)$ steps and I did some experiments which seem to confirm this.

(Note that picking a bin uniformly at random is a very different process that will obviously take $\Theta(n^2)$ steps to finish.)

Answer 1

Not really an answer, but an extended comment on András's answer.

András's answer contains a nice intuition, though I do not believe it is a rigorous calculation of the expected number of steps. I think it is perhaps a good approximation to an answer, but it does not seem to properly deal with cases where the bin below the highest occupied bin becomes empty before that the upper bin is emptied downwards. Still, this might be a reasonable approximation to make (I'm not sure).

His calculation contains an error which affects the scaling. I'm going to take exactly the same starting point, and redo and expand the calculation.

It misses a factor of p inside the summation, as the probability of randomly choosing the correct bin is $\frac{p}{n}$ rather than $\frac{1}{n}$. As a result we have

$\begin{eqnarray*} n + \sum_{p=1}^n \sum_{k=0}^{\infty} (k+1) \frac{p}{n} \left(\frac{n-p}{n}\right)^k & = & n + \sum_{p=1}^{n} \frac{p}{n} \sum_{k=0}^{\infty} (k+1) \left(\frac{n-p}{n}\right)^k \\\\& = & n + \sum_{p=1}^{n} \frac{p}{n} \cdot \frac{n^2}{p^2} \\\\& = & n + n\sum_{p=1}^{n} 1/p \\\\& = & n (1+H_n) \end{eqnarray*}$

where $H_n = \sum_{p=1}^{n} 1/p$ is the nth Harmonic number. To approximate $H_n$ we can simply replace the summation with an integral: $H_n \approx \int_{1}^{n+1} \frac{1}{x} dx = \log(n+1)$. Thus the scaling is $n (1+\log(n+1))$ or approximately $n \log(n+1)$. While this scaling does not match the scaling of the problem exactly (see simulation below) it is out by almost exactly a factor of $\log(2)$.

Red circles: Data points from simulation of process averaged over 10k runs. Green: $n \log_2(n+1)$. Blue: $n \log(n+1)$.

Answer 2

Edit: I am leaving this answer as is (for now) to illustrate the messy process of proving theorems, something that is left out of published papers. The core intuition here is that it is enough to focus on the top ball, as it sweeps away all below it. Please see the comments (in particular @Michael pointing out that gaps can occur) and @Joe's later answer for how errors were identified and corrected. I especially like Joe's use of experiments to double-check that the formulas were sensible.

---

The lower bound is $n$ as you point out, but somewhat surprising there seems to be an upper bound of $(1 + \pi^2/6)n$ for the expected number of steps.

To derive this, note that a sequence of balls will clear all the bins precisely if it contains a subsequence $b_1b_2\cdots b_n$ such that $b_1 = n$, $b_2 \ge n-1$, $\dots$, $b_i \ge n-i+1$. Additional conditions are necessary on the sequence to avoid balls being chosen that are no longer in the system, but for the purposes of an upper bound, suppose that there is an infinite decreasing sequence of bins (so the balls don't disappear when leaving bin 1, but are moved to bin 0, then bin -1, and so on). Then the expected number of steps for such a subsequence to be seen is the expected number of steps before $b_1$ is seen, plus the expected number of steps before $b_2$ is seen, and so on (down to 1, since $b_n$ can be any of the numbers $1,2,\ldots,n$). These can be seen as separate events, one after the other. The expected number of steps is then

$\begin{eqnarray*}n + \sum_{p=1}^n \sum_{k=0}^{\infty} \frac{k+1}{n} \left(\frac{n-p}{n}\right)^k & = & n + \sum_{p=1}^{n-1} \frac{1}{n-p} \sum_{k=1}^{\infty} k\left(\frac{n-p}{n}\right)^k \\& = & n + \sum_{p=1}^{n-1} \frac{1}{n-p} n(n-p)/p^2 \\& = & n + n\sum_{p=1}^{n-1} 1/p^2 \\& \le & (1 + \pi^2/6)n. \end{eqnarray*}$