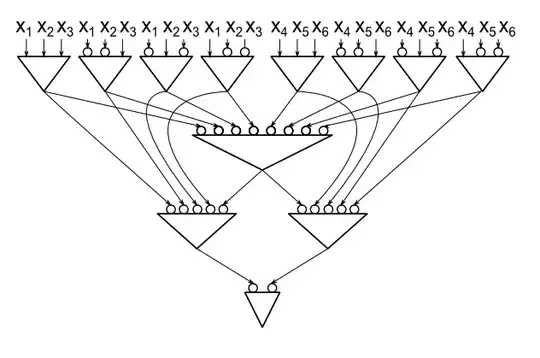
This gate-elimination lower bound does not match Marzio’s upper bound, but it’s a start.
Proposition: Every unbounded fan-in AND/OR/NOT circuit computing parity on $n\ge2$ variables contains at least $2n-1$ AND and OR gates.
For convenience, I will use a model where the only gates are AND-gates, but we allow negation wires. It is easy to see that $3$ gates are necessary for $n=2$, hence it is enough to show that if $C$ is a minimal-size circuit computing parity on $n>2$ variables, we can find a restriction of one variable which kills at least two gates.
If some variable $x_i$ has at least two positive parents (i.e., it is connected by unnegated wires to two different gates), setting this variable to $0$ will kill the parents and we are done; likewise if it has two negative parents. We may thus assume that each variable has at most one positive and at most one negative parent.
Let $a$ be a bottom-level gate in the circuit. Without loss of generality, $a=x_1\land x_2\land\cdots$. Set $x_1=0$, which forces $a=0$ and kills it. The restricted circuit $C'$ still computes parity, in particular it depends on $x_2$, hence $x_2$ has a negative parent $b=\neg x_2\land c_1\land\dots\land c_r$. Notice that in $C'$, no $c_j$ depends on $x_2$. If there were an assignment to $x_3,\dots,x_n$ which (on top of $x_1=0$) makes some $c_j$ false, the circuit restricted by this assignment would be constant, contradicting the fact that it computes $x_2$ or $\neg x_2$. Thus, in $C'$, all the $c_j$ compute constant $1$, and $b$ computes $\neg x_2$, hence we can eliminate it along with $a$.
EDIT: As I learned from Yuri Kombarov’s paper, this $2n-1$ lower bound, as well as the $\lfloor\frac52n\rfloor-2$ upper bound implied by Marzio De Biasi’s answer, were originally proved in
[1] Ingo Wegener, The complexity of the parity function in unbounded fan-in, unbounded depth circuits, Theoretical Computer Science 85 (1991), no. 1, pp. 155–170. http://dx.doi.org/10.1016/0304-3975(91)90052-4