12

Some time ago, I posted a reference request for graph problems where we want to find a 2-partition of the edges where both sets fulfill a property not related to their cardinality. I was trying to prove that the following problem is NP-hard:

Given a tournament $G = (V,E)$, is there a feedback arc set $F \subseteq E$ in $G$ that defines a transitive relation?

I do have a construction for an attempt at a proof, but it seems that that is going to run into a dead end, so I thought I might ask here to see whether I'm missing something obvious. In order to not confine your creativity to lines of thought similar to the ones I used, I won't post my attempt here.

Is this problem NP-hard? If so, how to prove it?

Community
  • 1
G. Bach
  • 431
  • 2
  • 17
  • Just to clarify possible questions: since $F \subseteq E \subseteq V^2$, $F$ itself is a relation (as is $E$). The question is, is there a transitive $F$ such that $(V, E \setminus F)$ is acyclic. – G. Bach Jan 20 '14 at 16:11
  • 1
    perfect, thanks! (I deleted the comment because I wrote G=(E,V) instead of the standard G=(V,E) :-) – Marzio De Biasi Jan 20 '14 at 16:13
  • 6
    If I understand correctly, this is equivalent to asking whether the edges in a tournament can be partitioned into two DAGs, one of which is transitively closed. – dspyz Jan 22 '14 at 02:51
  • @dspyz Yes, that would be another formulation of the problem. – G. Bach Jan 22 '14 at 13:29
  • idea: is it related somehow to a question on 2coloring edges or can it be stated more as a coloring problem... – vzn Jan 22 '14 at 23:48
  • @vzn I'm not sure how you could encode transitivity or acyclicity in colorings, but I may be missing something. – G. Bach Jan 23 '14 at 03:46
  • 1
    re dspyz's comment, there are not that many problems on DAGs that can be studied due to the complexity of them. there arent even that many theorems at all on DAGs it would seem. trees are a little more accessible. your problem (while apparently interesting as reflected in votes) seems to mix a lot of unusual elements together & not fit into any particular category. – vzn Jan 23 '14 at 03:59
  • A clarification question: Is it possible to partition a tournament into two DAGs efficiently? Or is this problem NP-hard? – Igor Shinkar Jan 23 '14 at 13:37
  • 5
    @IgorShinkar the arcs of any digraph can be partitioned trivially into two DAGs: order the vertices arbitrarily; one DAG is the forward edges, the other DAG is the backward edges. – Sasho Nikolov Jan 28 '14 at 00:00
  • An interesting question might be if you can partition the vertices of a digraph into two sets, so that the induced digraph on each of the sets is a DAG. But this problem is not very related to OP's question, which is about partitioning the arcs. – Sasho Nikolov Jan 28 '14 at 00:03
  • 1
    @SashoNikolov of course! – Igor Shinkar Jan 28 '14 at 07:08

3 Answers3

4

To add a little context, here's a construction for a graph that doesn't have a transitive feedback arc set. For this construction, I'll use the following gadget graph:

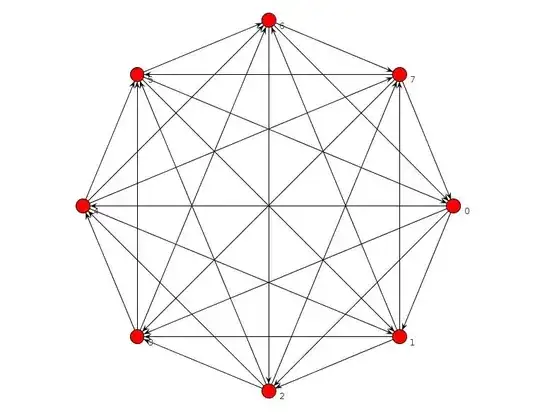
gadget graph used to force implications

This tournament has the following properties (which I checked using a program, I didn't prove it formally):

  • if (2,7) is not in a given TFAS, then (1,3) is
  • if (5,1) is in a given TFAS, then so is (3,6)
  • if (7,3) is in a given TFAS, then (5,1) is not

or slightly abusing predicate logic notation:

  • $\neg (2,7) \rightarrow (1,3)$
  • $(5,1) \rightarrow (3,6)$
  • $(7,3) \rightarrow \neg (5,1)$

You'll notice that for each implication, the two edges are pairwise disjoint, so the following construction works:

construction for graph that doesn't have a TFAS

I hope you can make out the idea of the graph: using the implication properties of the tournament above, we can construct a graph in which each transitive feedback arc set both includes and doesn't include the edge $A$, i.e. a contradiction, which means the graph doesn't have a transitive feedback arc set. Any completion of that graph cannot have one either since the same contradiction will remain in any completion. I left out a large number of vertices, all of which can be derived from substituting the tournament above for the implications.

G. Bach
  • 431
  • 2
  • 17
  • I'm sorry, I don't follow. Is there any reason you can't just post a list of the edges so I can run it through an ASP solver and try to verify it? According to clingo, your gadget graph has 8 different TFAS's. Here's the smallest one: tfas(edge(5,0)) tfas(edge(6,0)) tfas(edge(7,0)) tfas(edge(6,2)) tfas(edge(7,3)) tfas(edge(1,2)) tfas(edge(1,3)) tfas(edge(7,5)) – dspyz Jan 30 '14 at 04:13
  • I just noticed you mentioned the edge (6,3) in the gadget graph, but the image you provided has the edge (3,6) – dspyz Jan 30 '14 at 05:20
  • I figured it out, see my updated answer: http://cstheory.stackexchange.com/a/20778/13643 – dspyz Jan 30 '14 at 06:32
  • @dspyz I thought the construction was clearer than just a list of the edges, since if my reasoning isn't wrong, all that would be required to verify is whether the tournament above the construction actually has those implication properties. Thanks for pointing out the mistake about edge (3,6)! I also got 8 TFAS for that gadget, the one you listed being one of them. – G. Bach Jan 30 '14 at 14:02
  • I'm sorry. I constructed the graph wrong. I fixed it and clingo now reports no TFAS. – dspyz Feb 01 '14 at 19:10
  • @dspyz Thank you very much for putting this much effort into this! I was quite a bit confused since just like you, I couldn't see an error in the construction. At least that bit is settled, then. – G. Bach Feb 01 '14 at 20:02
  • I found one with nine vertices. See the updated answer – dspyz Feb 01 '14 at 22:51
1

I ran a short clingo program which reported no graph without a TFAS, but there was a bug. I fixed it and now it verifies there's no graph without a TFAS for n=8 or less. For n=9, it finds this one:

is_edge(edge(2,3)) is_edge(edge(1,4)) is_edge(edge(2,4)) is_edge(edge(3,5)) is_edge(edge(4,5)) is_edge(edge(1,6)) is_edge(edge(2,6)) is_edge(edge(3,6)) is_edge(edge(5,6)) is_edge(edge(1,7)) is_edge(edge(4,7)) is_edge(edge(5,7)) is_edge(edge(6,7)) is_edge(edge(1,8)) is_edge(edge(3,8)) is_edge(edge(4,8)) is_edge(edge(5,9)) is_edge(edge(6,9)) is_edge(edge(7,9)) is_edge(edge(2,1)) is_edge(edge(3,1)) is_edge(edge(4,3)) is_edge(edge(5,1)) is_edge(edge(5,2)) is_edge(edge(6,4)) is_edge(edge(7,2)) is_edge(edge(7,3)) is_edge(edge(8,2)) is_edge(edge(8,5)) is_edge(edge(8,6)) is_edge(edge(8,7)) is_edge(edge(9,1)) is_edge(edge(9,2)) is_edge(edge(9,3)) is_edge(edge(9,4)) is_edge(edge(9,8))

Here's the (fixed) encoding

% tfas.asp
#show is_edge/1.
vertex(1..n).

opp_edges(edge(A,B),edge(B,A)) :- vertex(A), vertex(B), A < B.
possible_edge(E1;E2) :- opp_edges(E1,E2).

{is_edge(E1); is_edge(E2)} = 1 :- opp_edges(E1, E2).
ntfas(E) :- possible_edge(E), not is_edge(E).
ntfas(edge(X, X)) :- vertex(X).

tfas(E) | fs(E) :- is_edge(E).
ntfas(E) :- fs(E).

broken :- ntfas(edge(A,C)), tfas(edge(A, B)), tfas(edge(B,C)).

reachable(X, Y) :- fs(edge(X, Y)), is_edge(edge(X, Y)).
reachable(X, Z) :- reachable(X, Y), fs(edge(Y, Z)), is_edge(edge(Y, Z)).
broken :- reachable(X, X).

tfas(E) :- broken, possible_edge(E).
fs(E) :- broken, possible_edge(E).
:- not broken.

Run it with clingo -c n=7 tfas.asp (Using clingo 4.2.1)

(the n=7 indicates graphs of exactly 7 vertices)

It should return satisfiable if and only if there exists a graph with no TFAS on 7 vertices.

Ok, I figured out what graph @G.Bach was describing and coded it up in clingo (see the clingo description below. It starts with a description of the gadget graph and proceeds to describe how to join copies of it together to get the full 34-vertex tournament graph G.Bach is describing. I've attached the grounded graph description as well).

I then proceeded to run clingo on that graph and it claimed to have found a TFAS with 241 edges. But I made a mistake in the graph encoding. I fixed the mistake and clingo now reports unsatisfiable (ie there is no TFAS).

Here's the program for finding TFAS's on a graph

{tfas(E)} :- is_edge(E).
:- not tfas(edge(A,C)), tfas(edge(A, B)), tfas(edge(B,C)).

reachable(X, Y) :- not tfas(edge(X, Y)), is_edge(edge(X, Y)).
reachable(X, Z) :- reachable(X, Y), not tfas(edge(Y, Z)), is_edge(edge(Y, Z)).
:- reachable(X, X).

tfas_count(N) :- N = #count{tfas(E) : tfas(E)}.

#show tfas/1.
#show tfas_count/1.

Here's the (updated) program for generating G.Bach's graph. I added indicators at the end to check that the graph is a well-formed tournament graph:

gadget_vertex(0..7).

gadget_edge(0,1).
gadget_edge(0,2).
gadget_edge(0,3).
gadget_edge(0,4).
gadget_edge(1,2).
gadget_edge(1,3).
gadget_edge(1,6).
gadget_edge(1,7).
gadget_edge(2,3).
gadget_edge(2,4).
gadget_edge(2,5).
gadget_edge(2,7).
gadget_edge(3,4).
gadget_edge(3,5).
gadget_edge(3,6).
gadget_edge(4,1).
gadget_edge(4,5).
gadget_edge(4,6).
gadget_edge(4,7).
gadget_edge(5,0).
gadget_edge(5,1).
gadget_edge(5,6).
gadget_edge(6,0).
gadget_edge(6,2).
gadget_edge(6,7).
gadget_edge(7,0).
gadget_edge(7,3).
gadget_edge(7,5).

special_edge(a;b;c;d;e).

forces(a,b).
forces(b,c).
forcesn(c,a).
nforces(a,d).
forces(d,e).
forces(e,a).

relates(A,B) :- forces(A,B).
relates(A,B) :- nforces(A,B).
relates(A,B) :- forcesn(A,B).

is_se_pair(se_pair(A,B)) :- relates(A,B).
vertex_name(v(V,P)) :- gadget_vertex(V), is_se_pair(P).

matches(from(A), v(5, se_pair(A,B))) :- forces(A,B).
matches(to(A), v(1, se_pair(A,B))) :- forces(A,B).
matches(from(B), v(3, se_pair(A,B))) :- forces(A,B).
matches(to(B), v(6, se_pair(A,B))) :- forces(A,B).

matches(from(A), v(2, se_pair(A,B))) :- nforces(A,B).
matches(to(A), v(7, se_pair(A,B))) :- nforces(A,B).
matches(from(B), v(1, se_pair(A,B))) :- nforces(A,B).
matches(to(B), v(3, se_pair(A,B))) :- nforces(A,B).

matches(from(A), v(7, se_pair(A,B))) :- forcesn(A,B).
matches(to(A), v(3, se_pair(A,B))) :- forcesn(A,B).
matches(from(B), v(5, se_pair(A,B))) :- forcesn(A,B).
matches(to(B), v(1, se_pair(A,B))) :- forcesn(A,B).

same_vertex(V, V) :- vertex_name(V).
same_vertex(M, N; N, M) :- matches(X, M), matches(X, N).

already_found(v(Y,N2)) :- vertex_name(v(X,N1)), same_vertex(v(X,N1),v(Y,N2)), N1 < N2.
vertex(V) :- vertex_name(V), not already_found(V).

named_gadget_edge(edge(v(X,SE),v(Y,SE))) :- gadget_edge(X,Y), is_se_pair(SE).
from_gadget_edge_named(edge(A, B), edge(C,D)) :- named_gadget_edge(edge(C,D)), same_vertex(A,C), same_vertex(B,D), vertex(A), vertex(B).
from_gadget_edge(edge(A,B)) :- from_gadget_edge_named(edge(A,B),edge(C,D)).
is_edge(E) :- from_gadget_edge(E).
is_edge(edge(A,B)) :- vertex(A), vertex(B), A < B, not from_gadget_edge(edge(B,A)).

vertex_count(VN) :- VN = #count{vertex(V) : vertex(V)}.
edge_count(EN) :- EN = #count{is_edge(E) : is_edge(E)}.

#show vertex_count/1.
#show edge_count/1.

bidirectional :- is_edge(edge(A,B)), is_edge(edge(B,A)).
phantom_vertex :- is_edge(edge(A,B)), not vertex(A).
phantom_vertex :- is_edge(edge(A,B)), not vertex(B).
incomplete :- vertex(A), vertex(B), not is_edge(edge(A,B)), not is_edge(edge(B,A)), A != B.

#show bidirectional/0.
#show phantom_vertex/0.
#show incomplete/0.
dspyz
  • 916
  • 4
  • 13
  • I'm positive there is a tournament on 18 vertices that doesn't have a TFAS. – G. Bach Jan 29 '14 at 19:07
  • Can you please give it as an example? Just attach a file with the edges listed – dspyz Jan 29 '14 at 19:08
  • How do I attach a file? It may take a few hours, I don't have the tournament to hand right now. I also miscalculated, it should have 34 vertices. It's probably easier to verify if I give the building blocks of the tournament. – G. Bach Jan 29 '14 at 19:25
  • Upload to any file host and link to it (see http://meta.stackexchange.com/a/4643/185877), or if it has a regular structure, just describe it (give the building blocks) – dspyz Jan 29 '14 at 19:29
  • cant follow your code yet but youre asserting that you are validating for finite n≤20? last sentence which asserts it is true for all $n$... if so quite remarkable(!) but not a "solution" to the general question (which would require a proof of all size cases). ps *thx* for working/posting an empirical observation to this site which in general is *rare* ... @G.Bach it would be great to see an image of the graph rather than just edge/vertex lists if possible – vzn Jan 30 '14 at 02:07
  • @dspyz I just posted an answer describing the construction of a tournament that doesn't have a transitive feedback arc set. I actually construct a digraph that isn't a tournament, but any completion of it cannot have a TFAS either. I'm sceptical you could have checked all isomorphism classes over 20 vertices; those should be an astronomically large number of tournaments. – G. Bach Jan 30 '14 at 02:17
  • @vzn I recognize this is not a solution, but I thought the OP would be interested to know this. Furthermore, the comment area doesn't provide enough space (or the ability to include newlines) to say this. Plus I saw your SWAG conjecture which is also not a solution, just a SWAG conjecture. And this lends support to it (although I'm still convinced there's a bug in clingo. I sent a message to the potassco mailing list asking them to take a look at this problem) – dspyz Jan 30 '14 at 04:20
  • @G.Bach Modern SAT solvers (or in this case ASP solvers) use techniques which allow them to prune large portions of the search space. This is why it's generally possible to solve SAT instances with up to thousands of variables. Despite not actually visiting every single tournament graph on 20 vertices (exactly 20, not up to 20, to check other sizes, you'll need to input other values of n), this code still checks if there exists one without a TFAS (or at least it should. As I mentioned I'm still somewhat skeptical that there might be a bug in this latest version of clingo). – dspyz Jan 30 '14 at 04:23
  • oops rereading & reinterpreting realize you mean in last sentence that the solver is solving one instance of the problem quickly or instances up to $n$ only, earlier interpreted it to mean that you'd solved the complete problem posed in the question (which relates to all $n$). yes of course the conjecture is not pretending to be any solution, just a "base of further operations", and stated in comments below its apparently false (GB states below he knew as much when he posted the question) – vzn Jan 30 '14 at 04:33
  • @vzn this code is probably easier to understand if you're familliar with the proof that disjunctive ASP is Sigma-2 complete (can't find a ref. right now). It follows the same pattern of asserting the disjunction a | b (in this case tfas | fs for each edge), and then having the negation of the clause (tfas is transitive and fs is acyclic) force both a and b so that the solution set is only minimal if the negation doesn't hold for any set of atoms (because all such sets would be subsets) – dspyz Jan 30 '14 at 04:42
  • it sounds like you need some way to validate the pruning that the algorithm is doing ie some kind of "debug output" that can be examined/ verified & isolate where mistake is being made if there is indeed bug, or rule out such a defect. dont know this system much but its an obvious design criteria that all its users would want/benefit from. thx for the ref to this code, it is the 1st have seen it on this entire site, looks very interesting, intend to delve into it further, looks powerful & like it could be used for all kinds of various problems/investigations.... – vzn Jan 30 '14 at 04:47
  • Actually, some newer ASP solvers can produce proofs when they return UNSAT. I don't know if clingo can. I sent an email to the potassco users mailing list asking them to take a look at this. If I could understand @G.Bach's counter-example graph, I would have much stronger evidence that there is indeed a bug. I could also probably use it to help trace the origin of that bug. – dspyz Jan 30 '14 at 04:50
  • how long does the $n=20$ case take to run? is that the highest $n$ youve tried? are there any papers that talk about doing induction based on the results for all $n<m$ and succeed, ie obtain actual proofs for all $n$? – vzn Jan 30 '14 at 04:53
  • It's all parsing/grounding time (which should be cubic in the number of vertices). At 100 vertices on my crappy old laptop, that's around 18 seconds. In all cases I've tried, the actual solving time seems to be negligible (hence my skepticism) – dspyz Jan 30 '14 at 04:57
  • Is there a way to extract just the edges from the TFAS that clingo produces? I'm very much interested to see this, especially since if the graph I described really does have a TFAS, then I can't see what's wrong with my reasoning that it shouldn't have one. – G. Bach Jan 30 '14 at 14:19
  • Yes, the edges are listed in http://wikisend.com/download/757898/tfas.res also I'm as confused as you are. As far as I can tell, your proof is sound. And I checked that your claim does indeed hold on the gadget graph (replacing (6,3) with (3,6)). I'll try to look into it a little deeper later. – dspyz Jan 30 '14 at 20:33
  • Also, sorry about the long wordy vertex names. They're an artifact of the way in which the graph was constructed – dspyz Jan 30 '14 at 20:35
0

SWAG conjecture [something better than nothing?]:

Given a tournament $G = (V,E)$, there exists a feedback arc set $F \subseteq E$ in $G$ that defines a transitive relation. hence the problem is $O(1)$

notes: shootdown counterexamples welcome! none seem to be given so far. even better would be some observations of patterns of edge orientations related to particular graph classes. or some more motivation or tieing it into some existing literature. offered in the style of Proofs and refutations (Lakatos)... also, since it seems such an offbeat problem that doesnt [yet?] relate to much, suggest studying it empirically....

vzn
  • 11,014
  • 2
  • 31
  • 64
  • 1
    I did run a program to check whether this holds and found that there are tournaments that do not have a transitive feedback arc set. I'll post one tomorrow, I won't get around to it today. – G. Bach Jan 28 '14 at 17:09
  • @vzn can you prove the conjecture for a random tournament? – Igor Shinkar Jan 28 '14 at 19:53
  • Counterexample with only 5 vertices: a->b, a->c, b->c, d->a, b->d, c->d, e->a, e->b, c->e, d->e. For any four vertices, the induced graph contains a cycle, so a transitive DAG can contain at most 3 edges among 3 vertices of the graph. There are only 5 possibilities (all other triplets are cycles): abc,eab,dea,bcd,cde It's easy to check that in each of the five cases there is a cycle among the other 7 edges – dspyz Jan 29 '14 at 06:31
  • Oh wait, I forgot that you can also include the edge between the other two vertices without breaking transitivity. Now I'm not sure – dspyz Jan 29 '14 at 06:37
  • 1
    Yeah, nvr mind, it's not a counterexample – dspyz Jan 29 '14 at 06:39
  • 1
    @dspyz I ran a brute force check on all tournaments on up to 8 vertices. All of them have transitive feedback arc sets, but there are some you can use to build a tournament that doesn't. – G. Bach Jan 29 '14 at 15:16
  • @dspyz / GB thx for further look & your further effort is interesting. the conjecture is almost not based on any analysis at all but merely a possibly easily-overturned "stake" to spur something further and an "empirical experiment" to see what will happen to the bounty/ dont want it to go to waste =D ... might be interested to put further thought/effort into this (like the DAG restatement) but feel there is insufficient bkg/motivation on it so far [am all open ears if gb would care to elaborate]... chat on it sometime anyone? – vzn Jan 29 '14 at 18:05
  • @vzn In case you're still curious, I posted an answer describing the construction of a tournament that doesn't have a transitive feedback arc set. – G. Bach Jan 30 '14 at 02:10
  • @g.bach interesting graph. new revised conjecture, for some $m$ all graphs $n<m$ vertices have a TFAS =D ... wonder if the pairwise disjoint edge/implication idea can generate all non-TFAS graphs... – vzn Jan 30 '14 at 02:16
  • @vzn I verified that conjecture for $m = 8$ when I was looking for that tournament I gave. – G. Bach Jan 30 '14 at 02:20
  • @g.bach ok did you know all this when you posted the question? if so itd be helpful to include it. – vzn Jan 30 '14 at 02:20
  • @vzn I did, but I purposely didn't include it because I was worried that information might get people stuck the same way it got me stuck. Not knowing something allows more creativity sometimes, at least that's what I thought. – G. Bach Jan 30 '14 at 02:22
  • @G.Bach agreed, sometimes, but it can also help solving the problem based on all/full info known so far and avoiding immediately wrong ideas such as the one posted...! also my revised conjecture cannot be proven/verified empirically, again due to same issue raised on dspyz's answer. or rather, meant to include also in the new conjecture that all $n>m$ have at least one non-TFAS graph. – vzn Jan 30 '14 at 02:24