26

Volume III of Knuth's The Art of Computer Programming (chapter 5, verse 3.2) includes the following table listing the exact minimum number of comparisons required to select the $t$th smallest element from an unsorted set of size $n$, for all $1\le t \le n\le 10$. This table, along with the well-known closed-form expressions $V_1(n) = n-1$ and $V_2(n) = n - 2 + \lceil n/2 \rceil$, represents most of the state of the art as of 1976.

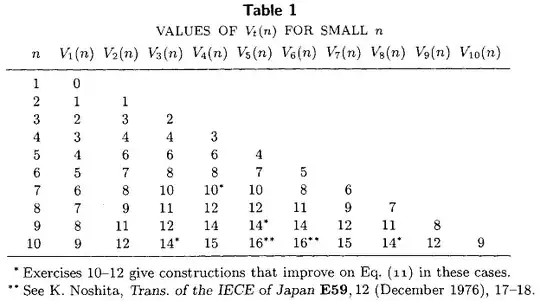
Table from Knuth III:5.3.2

Have any more exact values of $V_t(n)$ been computed in the last 36 years? I'm particularly interested in exact values of $M(n) = V_{\lceil n/2 \rceil}(n)$, the minimum number of comparisons required to compute the median.

As @MarkusBläser points out, Knuth's table seems to already incorporate more recent results from Bill Gasarch, Wayne Kelly, and Bill Pugh (Finding the ith largest of n for small i,n. SIGACT News 27(2):88-96, 1996.)

Jeffε
  • 23,129
  • 10
  • 96
  • 163
  • relevant? http://epubs.siam.org/doi/abs/10.1137/S0895480199353895 – Sasho Nikolov Aug 09 '12 at 18:38
  • Dor and Zwick's paper describes the best asymptotic results known for finding the median: $(2 + 2^{-80})n \le M(n) \le 2.95 n$. I'm more interested in exact values for small $n$. But it does include a reference to David Kirkpatrick's 1974 PhD thesis, which includes an exact bound for $V_3(n)$ for sufficiently large $n$ that I didn't notice before (and which Knuth didn't cite). – Jeffε Aug 09 '12 at 18:58
  • Actually, Knuth does cite Kirkpatrick's thesis, but claims a weaker result than Dor and Zwick. Specifically, Kirkpatrick's results imply exact values of $V_3(n)$ for infinitely many $n$. – Jeffε Aug 09 '12 at 19:11
  • 2
    The most famous paper on the topic, I think, is that of Pratt and Yao (1976) who are credited with being among the first to have found some (adversarial) technique to prove lowerbounds on this problem. If I were to find recent papers on the subject, I would follow citations made to this paper. The most recent paper is Dor and Zwick's, but there is also a 1996 survey by Paterson (though I have not looked to see if it concerns itself with exact results or not). – Jérémie Aug 10 '12 at 23:00
  • Patterson's survey is excellent, but it focuses on asymptotic results for large $n$. – Jeffε Aug 12 '12 at 13:19
  • 1
    Nitpicking: In the last sentence in the question, you probably meant the ceiling instead of the floor. – Tsuyoshi Ito Aug 12 '12 at 20:46
  • I just added the known values of $M(n)$ as a sequence on OEIS. – Jeffε Aug 13 '12 at 02:07
  • 6
    Jeff, curious why you are interested in the exact answer. – Chandra Chekuri Aug 13 '12 at 03:50
  • 1
    Some nitpicking: I think the table already contains the results by Gasarch, Kelly, Pugh from 1996 (SIGACT News 27, 2) – Markus Bläser Aug 13 '12 at 10:47
  • 5
    Kenneth Oksanen wrote an efficient code for computing $V_i(n)$. Unfortunately, there is only an abstract available http://www.sciencedirect.com/science/article/pii/S1571065306001582 Two years ago, one of my students send him an email and got the code from him. I do not remember whether some new values could be obtained. – Markus Bläser Aug 13 '12 at 10:50
  • 5
    @ChandraChekuri: I'm playing around with variants of the Blum-Floyd-Pratt-Rivest-Tarjan linear-time selection algorithm, as a potential algorithms homework problem. If we use the minimum-comparison algorithm to find the median in each block, then what block size gives us the best constant in the big-Oh? 9 is better than 7 is better than 5; what about 11? – Jeffε Aug 13 '12 at 11:26
  • @MarkusBläser: thanks for the great reference!! – Jérémie Aug 13 '12 at 22:45
  • can someone indicate if the sorting graphs are (presumably) DAGs? (or trees?) and is there some discussion of the effect of the difference anywhere? – vzn Sep 06 '12 at 15:15

2 Answers2

17

Kenneth Oksanen has published an expanded table of values up to $n=15$, based on his own computer search. Okansen also provides descriptions of the optimal comparison trees for most of the values he reports. Here's a screenshot of his table:

Kenneth Oksanen's bounds for selection

Thanks to @MarkusBläser for the lead!

Jeffε
  • 23,129
  • 10
  • 96
  • 163
3

I wonder if this piece of information might be useful to you. Unfortunately it does not provide any additional information to the question of this post, but is rather more in reply to your comment about what this was for (analyzing variants of QuickSelect).

The expected minimum number of comparisons, noted $v(n,t)$ or $v_t(n)$ is of course significantly easier to compute (with expectation taken uniformly over all permutations), $$v_t(n)=n+\min(t,n-t)+\text{l.o.t.}.$$

This result is not infrequently used, and in particular is the basis for the algorithms in "Adaptive Sampling for QuickSelect" by Martínez, Panario and Viola. The starting point of the paper is QuickSelect median-of-three, and then to ask: is it pertinent to systematically pick the median, when the element we seek has a relative rank much lower than n/2 or much higher than n/2?

In other words, suppose you are looking for the $k$-th element in a list of $n$ elements, and you are choosing your pivot from clusters of $m$ elements. Instead of taking the median ($m/2$), you will take $\alpha m$ where $\alpha = k/n$. They show this algorithm can, for the right choice of $m$ be practically more efficient than the median-of-three variant.

Jérémie
  • 638
  • 4
  • 12