19

I am interested in the "nearest" (and "most complex") problem to the Collatz conjecture that has been successfully solved (which Erdos famously said "mathematics is not yet ripe for such problems"). It has been proven that a class of "Collatz-like" problems is undecidable. However, problems that are vaguely similar such as Hofstadter's MIU game (resolved, but admittedly more of a toy problem) are indeed decidable or have been solved.

Related questions

Collatz Conjecture & Grammars / Automata

Community
  • 1
vzn
  • 11,014
  • 2
  • 31
  • 64

2 Answers2

26

An extended comment:

Collatz-like sequences can be computed by small Turing machines having few symbols and states. In "Small Turing machines and generalized busy beaver competition" by P. Michel (2004) (doi and closely related 2019 preprint update), there is a nice table that positions Collatz-like problems between decidable TMs (for which the halting problem is decidable) and Universal TMs.

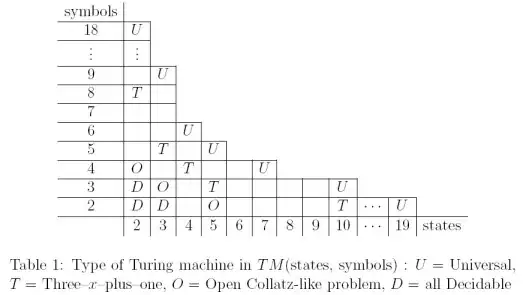
enter image description here

There are TMs that compute Collatz-like sequences for which the decidability is still an open problem: $TM(5,2)$, $TM(3,3)$ and $TM(2,4)$ (where $TM(k,l)$ is the set of Turing Machine with $k$ states and $l$ symbols). I don't know if the results have been inproved.

From the comclusion of the paper:

... The present Collatz-like line is already on its lowest possible level, with the possible exception of $TM(4,2)$, but we conjecture that all machines in this set can be proved to be decidable...

See also "The complexity of small universal Turing machines: a survey" by D. Woods and T. Neary (2007) (doi)

Another example of Collatz-like problem for which decidability is an open problem is the Post's tag system: $\mu = 2, v=3,0\rightarrow 00, 1 \rightarrow 1101$; for a recent analysis see "On the boundaries of solvability and unsolvability in tag systems. Theoretical and Experimental Results" by L. De Mol (2009).

Joshua Grochow
  • 37,260
  • 4
  • 129
  • 228
Marzio De Biasi
  • 22,915
  • 2
  • 58
  • 127
  • 9
    to complement the answer: Conway showed that there are Collatz-like sequences which are undecidable http://www.ams.org/mathscinet-getitem?mr=392904. i.e. a collatz-like sequence can itself simulate a universal turing machine. – Sasho Nikolov Jun 02 '12 at 16:23
  • thx! the mitchell survey/results are very cool! fyi clarification in the table, a "T" in a cell indicates a TM(k,l) has been shown to exist that is equivalent to the collatz conjecture. the perspective also suggests that the collatz conjecture is not merely an isolated theoretical curiosity but possibly a surface phenomenon of something deeper in computability theory. ps also very interested if any once-open "collatz like problems" have ever been solved...? – vzn Jun 02 '12 at 16:23
  • The TM(19, 2) Universal entry of the table has (since?) fallen to TM(15, 2) as per image at: https://cstheory.stackexchange.com/questions/10207/whats-the-simplest-noncontroversial-2-state-universal-turing-machine/10390#10390 – Ciro Santilli OurBigBook.com Sep 23 '23 at 10:28
5

Consider the function $T: \mathbb N \rightarrow \mathbb N$, where $T(n)=n/2$ when $n$ is even and $T(n)=n+1$ when $n$ is odd. Then it is known that for any $n \in \mathbb N$, there exists a $k \in \mathbb N$ such that $T^{(k)}(n)=1$.

If instead of $T(n)=n+1$ when $n$ is odd, we had defined $T(n)=3n+1$ when $n$ is odd, we would have the Collatz Conjecture, so I think this is the nearest problem to the Collatz Conjecture that has ever been resolved.

Craig Feinstein
  • 515
  • 6
  • 14
  • 2
    I don't think this satisfies the "most complex" part of the question, as a motivated grade school student can identify the key idea behind the proof of your statement with a bit of thought. – Yonatan N Jul 14 '15 at 22:17
  • 2
    But if it is more complex and still resolved, it won't resemble the Collatz Conjecture anymore. Furthermore, the title of his question indicates that he gives priority to "nearest" over "most complex". – Craig Feinstein Jul 15 '15 at 14:25