5

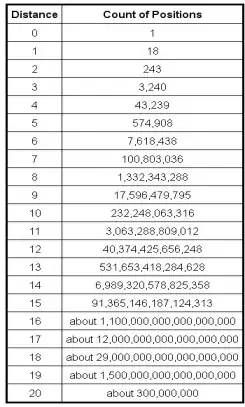
I saw a previous question about local maxima for the number of moves in a Rubik's cube solution, and I wondered what is known about the distribution of shortest paths when randomly scrambling a Rubik's cube.

  1. If I were to pick a (solvable) configuration at random, how far is it to the solved state?
  2. How many random moves does it take to sufficiently scramble the cube?

For the second question, I'm thinking of it as the mixing time, like for the Diaconis 7 shuffle result for a deck of cards. (Perhaps this is the wrong terminology?)

This is related to another question of mine about adversarially scrambling a Rubik's cube.

Edit: I accepted Marzio's answer, though I still wonder about the mixing time. Google revealed some results for particular finite groups, but I didn't see anything about Rubik's cube. Maybe one of these is applicable / can be ported over?

Community
  • 1
Lucas Cook
  • 255
  • 2
  • 7

1 Answers1

5

At God's number is 20 site you can find a nice distance/count table:

enter image description here

"... Distance-20 positions are both rare and plentiful; they are rarer than one in a billion positions, yet there are probably more than one hundred million such positions. We do not yet know exactly how many there are. The table on the right gives the count of positions at each distance; for distances 16 and greater, the number given is just an estimate. Our research has confirmed the prior results for entries 0 through 14 below, and the entry for 15 is a new result, which has since been independently confirmed by another researcher ...."

According to the table if you pick a random configuration it will be with high probability at distance 17-18 from the solution.

See also D. Joyner's notes Mathematics of the Rubik's cube (and D. Joyner's book "Adventures in Group Theory: Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys")

Marzio De Biasi
  • 22,915
  • 2
  • 58
  • 127
  • 1
    You are mixing up the diameter with the mixing time. – Tsuyoshi Ito May 09 '12 at 12:52
  • @TsuyoshiIto: you're right, I edited it trying to save it. – Marzio De Biasi May 09 '12 at 13:52
  • @MarzioDeBiasi Thanks for the link. Nice to see the data. – Lucas Cook May 10 '12 at 00:58
  • 1
    @LucasCook: but as commented by Tsuyoshi I didn't answer your second question. It probably involves applying randomly a generator for the group $G$, but I don't know if it's enough to pick uniformly at random a generator (simple random walk) and how many times. Perhaps the question can be generalized to Cayley graphs and re-asked here or on cs.stackexchange.com (I don't think it's research level). – Marzio De Biasi May 10 '12 at 08:21