4

This answer to another question describes the different values chosen as private key and public key by various Ed25516 implementations. What are the advantages / disadvantages of each?

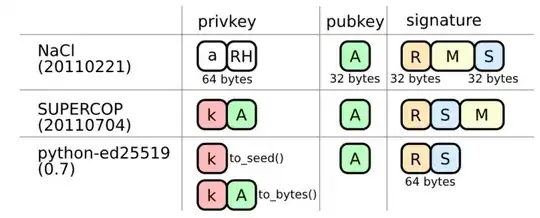
Different Ed25519 private key and signature formats for NaCl, SUPERCOP and python-ed25519

(Table cropped from diagram in the linked answer, originally taken from "How do Ed5519 keys work?" by Brian Warner.)

Community
  • 1
Charles Nobbert
  • 43
  • 4
  • I don't really get your question. Which different methods are you talking about? if you don't have any special requirements you should simply follow the spec, which derives the private scalar and a second key by hashing a 32 byte seed with SHA-512. – CodesInChaos Jul 24 '13 at 15:47
  • 2
    I think you are confused. The table on the bottom of the picture describes various APIs, but they implement the same cryptographic scheme. – orlp Jul 24 '13 at 16:30
  • 1
    I disagree; the table does show differences in what makes up 'a private key'. Now, the differences are fairly minor; however asking for someone to explain those differences would appear to be relevant. – poncho Jul 24 '13 at 18:24
  • @poncho Those differences are only memory/cpu time tradeoffs and all functionally equal. – orlp Jul 24 '13 at 20:34
  • @poncho. You are correct, I'm asking about the pros/cons of using a/RH vs k/A as the private key. – Charles Nobbert Sep 07 '13 at 18:34

1 Answers1

3

To perform an Ed25519 signature operation, you need to know three values, denoted by $\sf RH$, $a$ and $A$ in the diagram. Now, as it happens, these values are not independent:

  • $A$ can be derived from $a$, and
  • both $\sf RH$ and $a$ can be derived from the seed $k$.

Thus, all you really need to store is the seed $k$; everything else can be derived from it. Alternatively, it's possible to store $\sf RH$ and $a$ like NaCl does, which saves you the (minor) effort of one SHA-512 hash computation whenever you need to sign something.

There's no particular need to store the public key $A$ as part of the private key, since it can be derived from $a$ and you need to know $a$ anyway to be able to sign. However, deriving $A$ from $a$ requires an elliptic curve multiplication, which is a reasonably expensive operation compared to the other key generation steps. Thus, also storing $A$ as part of the private key provides a modest performance gain compared to storing just $k$ or just $\sf RH$ and $a$.

Community
  • 1
Ilmari Karonen
  • 46,120
  • 5
  • 105
  • 181