I was looking a Wikipedia article on SHA-2, and the "Comparison of SHA functions" table seems to indicate that SHA-2 is less secure than SHA-1.
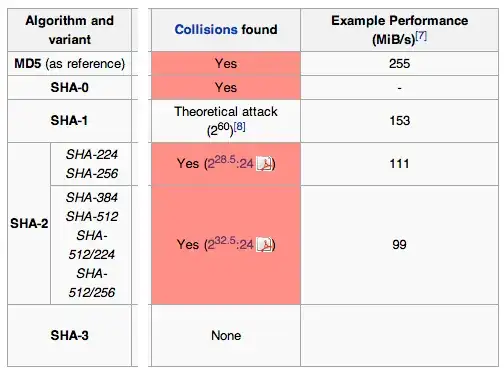
Is this true, or is the table wrong / misleading?
What does $2^{28.5}$ mean for SHA-256 compared to $2^{60}$ for SHA-1 (table in SHA-1 article says $2^{53}$)? How does it relate to MD5 article, which says:
The security of the MD5 hash function is severely compromised. A collision attack exists that can find collisions within seconds on a computer with a 2.6 GHz Pentium 4 processor (complexity of $2^{24.1}$)
Assuming that no collisions have been found for the SHA-2 family, does that still mean it takes less work to find a collision than SHA-1? Or do these numbers ($2^{28.5}$, $2^{60}$, $2^{53}$, $2^{24.1}$) mean different things?
If the table is wrong, how should it be corrected?
:24is probably referring to a version reduced to 24 rounds. – CodesInChaos May 20 '13 at 23:01