My understanding of duplex construction is usually initialized with the key at the beginning of the mode, but I have noticed that TinyJambu (in addition to key intilization) is using key in each processing call (keyed permutation) as shown in figure.
my questions : Is there a particular advantage of keyed permutation in duplex construction than an unkeyed permutation ?
There is indeed an advantage but it only makes sense if you understand how the initialization stage works.
TinyJambu is generally designed for a hardware implementation with a fixed key, and the key also burned into the hardware. Think an IOT device that reports data, but where there is a chance of theft and you dont want the key extracted, as the attacker has copies of all the ciphertext. Even worse, the attacker may want to forge messages.
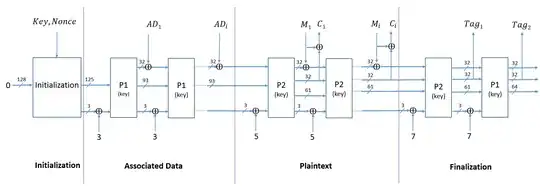
TinyJambu uses a single keyed permutation $P$ based on a NLFSR, this is iterated a number of times depending on how it is used and how large the key is. $P_n$ refers to the permutation iterated $n$ rounds. Note the diagram P1 and P2 are NOT $P_1$ and $P_2$, but rather a permutation step where $n$ is based on key size.
In the initialization stage, the key is not added to the state by XOR like in a typical sponge based cipher, rather it is permuted using $P_{1024}$, this effectively mixes the key into the state, but allows the key to stored only as part of the permutation.
After the state is keyed, the nonce is added 32-bits at a time. First a domain separator bit is added to the state, then it is permuted with $P_{384}$, then a nonce word is XOR'd. Once again the permutation is keyed here, so there is additional key mixing into the initial state.
In P1 and P2, P1 is equal to $P_{384}$, and P2 is $P_{1024}$ or larger, based on key size, in 128 round increments. The nonce is basically added using P1, just like the AD. Additionally, since the AD comes after the nonce, it changes the state in the same way, so nonce reuse with different AD does not compromise security.
So back to the question, what is the advantage of keyed permutation in duplex construction? Primarily to keep the state small, but also to make the cipher lightweight, as all key addition and permutation are part of a single operation. The designers also say:
When a key is already stored in the device, the state of the cipher could be very small since we can use the keyed permutation to prevent an attacker from computing the states offline and launching the state collision attacks using the computed states
With a state size of only 128-bits, it is possible (not probable) to compute the keyed initial state in advance and crack the whole cipher, but making the permutation keyed makes that even more infeasible.
