Probability distribution of bitwise-&

Question

Does the bitwise-& between two uniformly distributed input produce an output that seems uniformly distributed ? To be more specific, assume to take x and y uniformly from {0,1}^n and compute z = x & y. Assume then to uniformly choose a w from {0,1}^n. Do z and w have the same distribution over {0,1}^n ?

Take the case $n=1$ and compute the probability of the output depending of the different inputs. That should give you a beginning of an answer. — , Jul 06 '19 at 18:10

score 3 · Accepted Answer · answered Jul 06 '19 at 18:44

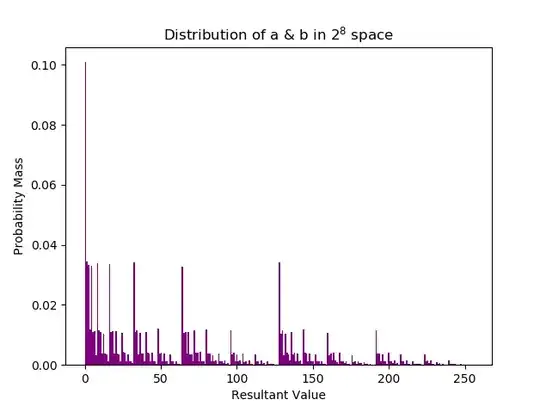
Not very. A few lines of code produces this for a & b with both variables uniformly distributed across $2^8$:-

I don't think that it has a specific distribution name, other than a classic "bitwise AND function".

From :-

for x in range(256 * 256):
    a = random.randrange(pow(2, 8))
    b = random.randrange(pow(2, 8))
    results.append(a & b)

Probability distribution of bitwise-&

1 Answers1