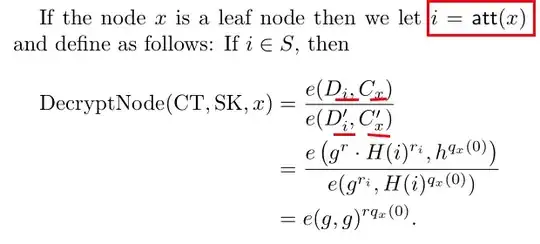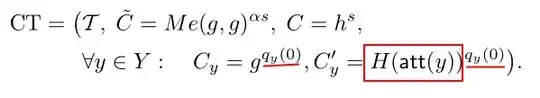Suppose that Alice has attributes A, B and C. I have a ciphertext with this policy: A AND C.
Can an adversary guess the attributes and then decrypt the ciphertext? What is the probability of guessing attributes in a ciphertext policy attribute based encryption?
In CP-ABE, the policy (i.e. which attributes are required to decrypt) is usually public. So Alice knows whether her A, B, C satisfy the policy or not. If not, Alice knows for example, D and E are required, but she does not have. She does not need to guess. She cannot decrypt the ciphertext however, because she does not have the private key corresponding to the missing attributes. The private keys are issued by a trusted party who will only issue to keys after verifying the requesting party does possess the attributes.
The legitimate recipient Alice of a CP-ABE ciphertext must somehow match her attributes secret key components ($D_i$ and $D'_i$) to the used attribute components in the access structure ($C_i$ and $C'_i$). For example in Bethencourt 2007:
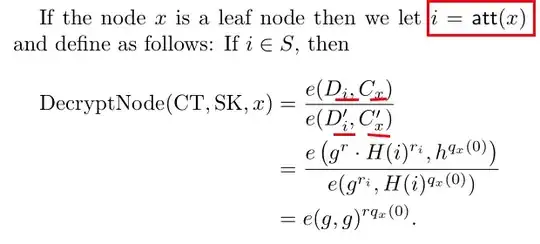
If Alice didn't know which of their $D$ would be correct for $C$ in the access structure, she would need to brute force this matching. This can be quite costly if there are many attributes at play, so real world implementations also add this metadata into the access structure.
Then you might ask is brute forcing the only way? For Bethencourt it is, because the hash ($H$) of the textual attribute representation (red box) is blinded by leaf node secret which is derived from the root secret. If you can unblind the hash in order to brute force the textual representation, then you don't need to do that anymore, because you already broken CP-ABE.
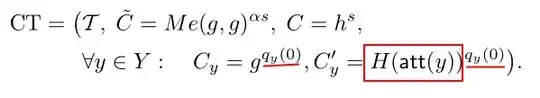
Aside from traditional CP-ABE, there are also constructions which attempt to remedy that by making the attributes in a ciphertext unguessable. Here are a few for self-study (in no particular order):
Han, 2014, PPDCP-ABE: Privacy-preserving decentralized ciphertext-policy attribute-based encryption
Okamoto, 2010, Fully secure functional encryption with general relations from the decisional linear assumption
Zhou, 2015, Efficient Privacy-Preserving Ciphertext-Policy Attribute Based-Encryption and Broadcast Encryption
Lai, 2012, Expressive CP-ABE with Partially Hidden Access Structures
