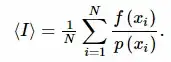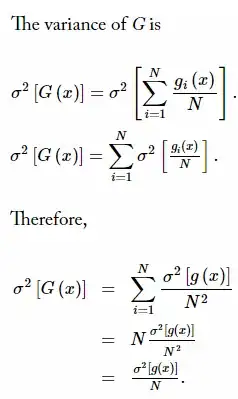So I was reading this paper by Lafortune, "Mathematical Models and Monte Carlo algorithms" and in it he writes.
We have a function or integrand I we want to estimate given as,
$I = \int f(x) dx$
We then have a primary estimator for this as,
$\hat{I_p} = f(\xi)$
where $\xi$ is a random number generated in the interval of the integrand $I$.
The secondary estimator is defined as,
$\hat{I_{sec}} = \frac{1}{N} \sum f(\xi_i)$
Then there is an explanation that goes to show how the expected value of the secondary estimator is equal to the function/integrand I. i.e,
$E(\hat{I_{sec}}) = I$
All fair. The problem comes when he tries to find the variance of this secondary estimator as follows. Im posting a screenshot of the paper here since it's getting a little complex.
I don't understand how did step 2 follow from step 1 of Equation 3.5 in the variance calculation. Note that he has assumed $PDF = 1$ for now
I was trying to calculate the variance using a more standard approach and ignoring the multiple integrals. We know the variance of an estimator $\hat{\theta}$ is given as
$Var(\hat{\theta}) = E[(\hat{\theta} - E(\hat{\theta}))^2]$
If we apply this to above we get
$Var(\hat{I_{sec}}) = E[(\hat{I_{sec}} - E(\hat{I_{sec}}))^2] $
$\hspace{20mm} = E[(\hat{I_{sec}} - I)^2]$
$\hspace{20mm} = E[(\hat{I_{sec}})^2 - 2* I *(\hat{I_{sec}}) + I^2 ] $
$\hspace{20mm} = E[(\hat{I_{sec}})^2] - 2* I *E[\hat{I_{sec}}] + I^2 $
$\hspace{20mm} = E[(\hat{I_{sec}})^2] - 2* I^2 + I^2$
$\hspace{20mm} = E[(\hat{I_{sec}})^2] - I^2 $
$\hspace{20mm} = E[(\frac{1}{N} \sum\limits_{i=1}^{N} f(\xi_i))^2] - I^2$
Now I am stuck here, I could do this,
$\hspace{20mm} = E[\frac{1}{N^2} \sum\limits_{i=1}^{N} f^2(\xi_i) + \frac{1}{N^2}\sum\limits_{i\neq j}^{N} f(\xi_i) f(\xi_j) ] - I^2 \hspace{10mm} \because [\sum\limits_{i=1}^{N} f(x_i) ]^2 = \sum\limits_{i=1}^{N} f^2(x_i) + \sum\limits_{i\neq j}^{N} f(\xi_i) f(\xi_j)$
$\hspace{20mm} = \frac{1}{N^2} \sum\limits_{i=1}^{N} E[f^2(\xi_i)] + \frac{1}{N^2}\sum\limits_{i\neq j}^{N} E[f(\xi_i) f(\xi_j) ] - I^2$
$\hspace{20mm} = \frac{1}{N^2} \sum\limits_{i=1}^{N} \int f^2(x)dx + \frac{1}{N^2}\sum\limits_{i\neq j}^{N} E[f(\xi_i) f(\xi_j) ] - I^2$
$\hspace{20mm} \because E[f(X)] = \int f(X) p(X) dx$
Note $p(X) = 1$,
$\hspace{20mm} = \frac{1}{N} \int f^2(x)dx + \frac{1}{N^2}\sum\limits_{i\neq j}^{N} E[f(\xi_i) f(\xi_j) ] - I^2$
Don't know what to do next from here, any tips? Or did I do something wrong?