4

Let's assume I have the following cube.

enter image description here

Let's assume the isovalue = 0. I would like to draw the resulting triangles of the isosurface.

I know that first I define which values are inside or outside comparing them to the given isovalue and after that we correspond to a particular list of edges.

After that, we have somehow to linearly interpolate the points. I have read on an article that using this formula $P = P_1 + \frac{(iso -V_1)(P_2-P_1)}{V_2-V_1}$ we can get the interpolated values.

Can someone demonstrate to me how I can interpolate the points in this case ?

john john
  • 423
  • 1
  • 3
  • 9

2 Answers2

2

P1 and P2 in this case represent the actual coordinates of the vertices of the cube in your output mesh. These might be the same as the input coordinates of the function you're using, or they might not be, it's entirely up to you how you output them. A simple way to map them would be to just use integer coords, biased by half the resolution of your sample volume - so a mesh spanning 100^3 cubes would have coordinates from -50 to 50 on each axis.

So in the formula you describe, (iso - V1) / (V2 - V1) gives you the amount to interpolate by, and (P2 - P1) is a vector representing a single cube lattice edge along the axis you want.

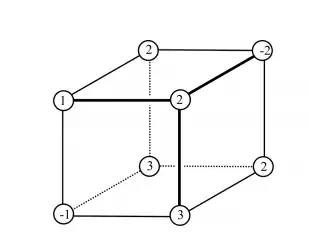
Let's assume we're using unit sized cubes, +Y is up, and +Z is 'into' the screen.

In your cube above, you will have crossings on the three edges coming from the left-bottom-front corner. On the X and Z edges you will interpolate by 0.25 : (0 - (-1)) / (3 - (-1)) , and on the Y edge you will interpolate by 0.5.

So if the left-bottom-front corner is at the origin, your three mesh vertices will be at <0.25, 0, 0> , <0, 0.5, 0> and <0, 0, 0.25>.

Apply the same formula to the right-top-back corner and you get <0.5, 1, 1>, <1, 0.5, 1> and <1, 1, 0.5>

The only difference is the left-bottom-front corner values will be P1 and V1 in your formula as it is at the 'negative' end of the edges to be interpolated, and the right-top-back values will be P2 and V2 as it is at the 'positive' end.

Hope that all makes sense.

russ
  • 2,392
  • 9
  • 18
  • 1
    I do not understand what you mean though in the last paragraph. Could you elaborate more on that ? For example, what do you mean by 'negative' and 'positive' end ? – john john May 27 '16 at 09:02
  • Say your cube is at position 0 on each axis in your volume, then it will fill the space from position 0 to position 1. So the left side of your cube will be at X=0 and the right side will be at X=1, same for the other two axes. So you use P1 and V1 for the edge end with the lower coordinate value and P2 and V2 for the end with the higher value. – russ May 30 '16 at 07:30
1

You can use this formula on each edge where one point is < isovalue and the other is > . Then you link together the points belonging to the same square to form the edges of your iso-mesh. Then you make polygons by linking edges sharing a vertex. In case of more than 3 sides (could be up to 6), it's up to you to prefer spliting the polygon into triangles.

Fabrice NEYRET
  • 1,266
  • 8
  • 14
  • could you apply your thinking to my example as stated above? I did not get the grasp of your method. – john john May 26 '16 at 09:00
  • If fact I'm not sure what you meanhere by "interpolate". If what you aim at is a mesh, your formula directly give the position where the isoval cross an edge. Then you obtain the mesh by connecting these points. – Fabrice NEYRET May 26 '16 at 15:50
  • What I do not understand, is where you put what in the formula. I know that in V1 and in V2 I should replace the values from the vertices but in P1 and P2 I have no clue what I should put there? Can you give me a hint how it works in the current example? – john john May 27 '16 at 08:08
  • P1 and P2 are the coordinates of the segment extremities. – Fabrice NEYRET May 27 '16 at 11:18