5

I encountered this problem doing my project. Suppose there is a 3D mesh model, e.g. a human face, I need the 3D visibility map at each of the vertices of this model. By the "3D visibility map", I mean the binary image covering the spherical surface indicating whether the point is visible from each spherical angle(different from ambient occlusion). So, it is like a mask image. For example, the visibility map for any point on a convex surface is all ones (occlusion by other objects is ignored, only self-occlusion). See the following figure for illustration

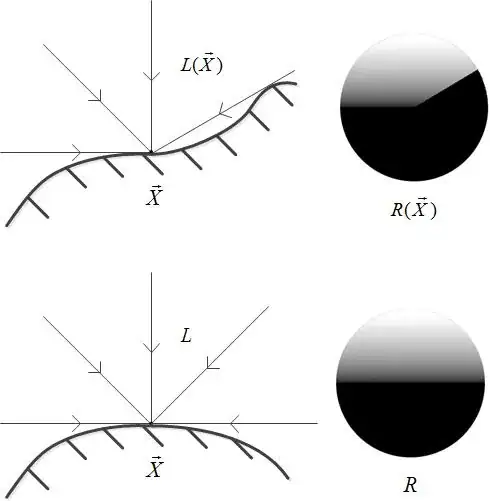
spherical visibility map in two cases

I want to know is there some efficient ways solving this problem? I need to apply it to all vertices. All I have in mind is doing brute force verification for all sampling directions. What's more, is there any existing software or tool (e.g. pbrt, Unity, Blender) that is capable of this functionality? Any suggestions and links are welcome. Thanks!

user1692
  • 53
  • 4
  • owell it is possible to do this analytically for polygons. Turn each poly into polar coordinates. You can then either analytically render these or sample like any other polygon, except they are now curved. Samplig may be faster though. – joojaa Sep 21 '15 at 19:25
  • Thanks for your comment @joojaa, but I cann't get your point. I intend to get the viewing field for each vertex (why do you mention "polygons"?). Is this what you mean: make each vertex as coordinate origin; then express all other vertices in polar coordiates (theta, phi, r) according to this origin; then do some analytical analysis using these coordinates or do sampling? Could you please make it more clear? – user1692 Sep 22 '15 at 01:45
  • 1
    Possibly relevant reading: Interactive Horizon Mapping. The visibility maps you describe are similar to what are called horizon maps in the literature, which store the elevation angle of the "horizon" for a predefined set of directions around each point on a surface. That paper is mainly about using them at runtime, though, with not much detail on generating them. – Nathan Reed Sep 22 '15 at 06:18

1 Answers1

3

This can be done analytically at least for polygonal meshes. You can convert points into polar coordinates and project on a sphere. Edges form planes that pass through projection circles center forming circles on the sphere. These lines are all great circles, because they must pass sphere center. Great circles form linear interpolations in polar coordinates.

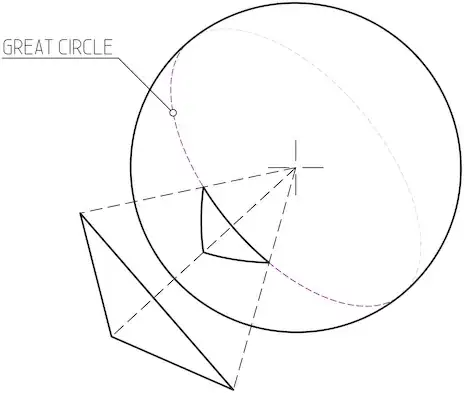
Project triangle on sphere

Image 1: Projecting a geometry on a sphere.

Converting these great circles into either Cartesian coordinates is quite well known math. Projecting them onto 2d representation by Mercator projection is well known math on account fo this being central to map making. Since overlap is not a problem you can just slap these triangles on top of each other and merge the vector results. Or use the polar coordinates for pixel graphics and even use z buffered overlap just like a normal camera.

The only problematic point is the one where your sphere is generated (if its on a open face edge). You can simply project the point on center into its inverse normal direction on the projection sphere. Or if for example Mercator projection is desired, you can align the sphere with surface normal. then just project them to a point on the south pole.

You can even interpolate the results of individual polygons positions to get any point on the triangle. And a analytic surface coverage for the triangle.

I haven't implemented this, but Ive done it manually a few times* so i know its possible. Should be pretty easy to do as the maths involved aren't all that complicated only problem is solving which side of the problem to keep.

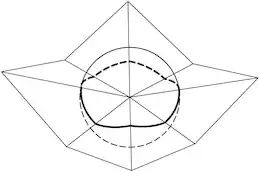
Local horizon map

Image 2: Horizon map of a simple all local geometry.

Comparison with raytracing

Both sampling triangles analytically is O(N) algorithm, if vector data is sufficient. Conditioning this data may push you over to O(N^2). Raytracing is O(N log(N)). Raytracing algorithms are easier to find of the shelf so implementing analytic polygon to sphere rendering is harder. In terms of speed analytical rendering is faster as long as theres a limited number of triangles, much like how scanline rendering is still sometimes faster than tracing despite being algorithmically more complex. This similarity is not just a coincidence it can be shown that this method can be turned into a scanline renderer.

Resources for drawing great circles in Mercator projection:

* About 20-25 times. I also did it for this image (yes in 3d), its as accurate as a single span Bezier curve can represent a circle. Ive also done this in map making software a few times.

joojaa
  • 8,437
  • 1
  • 24
  • 47
  • Thanks @joojaa. I think I understand your point now. So, basically, your method is to project the whole polygon sets to a unit sphere that is located at a observer point. Then, the spherical field that is covered by the projected polygons is not visible, right?

    This is an analytic method that gives the precise result. I think when apply this to all vertices, at each vertex I need to project to whole polygon set. So, this maybe computational heavy.

     – user1692 Sep 23 '15 at 06:23
  • Depends on how many polygons you have. You can do all the tricks of scanline rendering. And backface cull etc. In fact you can do this with normal hardware all you need to do is duplicate the triangles on the wrapping seams. So all things that apply for normal perspective projection apply here. This may be faster than raytracing extremely many rays though. – joojaa Sep 23 '15 at 06:28
  • Strictly from a CS perspective both raytracing and polygon projecting has a O(N) complexity its just that N is dramatically smaller for the polygon projection method. So your raytracer shoots 1-8 rays at the cost of one analytic polygon. – joojaa Sep 23 '15 at 06:37